2 dice are thrown. Suppose a random variable X is assigned a value 2k, if the sum on the dice is equal to k, then the expected value of X is
10
12
14
509
The correct Answer is:C
To solve the problem, we need to find the expected value of the random variable X defined as X=2k, where k is the sum of the numbers on two thrown dice.
1. Identify the Sample Space:
When two dice are thrown, the total number of outcomes is 6×6=36. Each die has 6 faces, so we can represent the outcomes as ordered pairs (d1,d2) where d1 and d2 can take values from 1 to 6.
2. Calculate the Possible Sums:
The possible sums k when rolling two dice range from 2 (when both dice show 1) to 12 (when both dice show 6). The sums can be calculated as follows:
- k=2: (1,1)
- k=3: (1,2), (2,1)
- k=4: (1,3), (2,2), (3,1)
- k=5: (1,4), (2,3), (3,2), (4,1)
- k=6: (1,5), (2,4), (3,3), (4,2), (5,1)
- k=7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
- k=8: (2,6), (3,5), (4,4), (5,3), (6,2)
- k=9: (3,6), (4,5), (5,4), (6,3)
- k=10: (4,6), (5,5), (6,4)
- k=11: (5,6), (6,5)
- k=12: (6,6)
3. Determine the Probability of Each Sum:
We can summarize the probabilities for each sum k:
- P(k=2)=136
- P(k=3)=236
- P(k=4)=336
- P(k=5)=436
- P(k=6)=536
- P(k=7)=636
- P(k=8)=536
- P(k=9)=436
- P(k=10)=336
- P(k=11)=236
- P(k=12)=136
4. Assign Values to the Random Variable X:
The random variable X is defined as X=2k. Therefore, the values of X corresponding to each k are:
- For k=2, X=4
- For k=3, X=6
- For k=4, X=8
- For k=5, X=10
- For k=6, X=12
- For k=7, X=14
- For k=8, X=16
- For k=9, X=18
- For k=10, X=20
- For k=11, X=22
- For k=12, X=24
5. Calculate the Expected Value E(X):
The expected value E(X) is calculated as follows:
E(X)=∑(Xi⋅P(ki))
Plugging in the values:
E(X)=4⋅136+6⋅236+8⋅336+10⋅436+12⋅536+14⋅636+16⋅536+18⋅436+20⋅336+22⋅236+24⋅136
Calculating each term:
=436+1236+2436+4036+6036+8436+8036+7236+6036+4436+2436
=50436
Simplifying gives:
E(X)=14
Final Answer:
The expected value of X is 14.
When two dice are thrown, the total number of outcomes is 6×6=36. Each die has 6 faces, so we can represent the outcomes as ordered pairs (d1,d2) where d1 and d2 can take values from 1 to 6.
The possible sums k when rolling two dice range from 2 (when both dice show 1) to 12 (when both dice show 6). The sums can be calculated as follows:
- k=2: (1,1)
- k=3: (1,2), (2,1)
- k=4: (1,3), (2,2), (3,1)
- k=5: (1,4), (2,3), (3,2), (4,1)
- k=6: (1,5), (2,4), (3,3), (4,2), (5,1)
- k=7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
- k=8: (2,6), (3,5), (4,4), (5,3), (6,2)
- k=9: (3,6), (4,5), (5,4), (6,3)
- k=10: (4,6), (5,5), (6,4)
- k=11: (5,6), (6,5)
- k=12: (6,6)
We can summarize the probabilities for each sum k:
- P(k=2)=136
- P(k=3)=236
- P(k=4)=336
- P(k=5)=436
- P(k=6)=536
- P(k=7)=636
- P(k=8)=536
- P(k=9)=436
- P(k=10)=336
- P(k=11)=236
- P(k=12)=136
The random variable X is defined as X=2k. Therefore, the values of X corresponding to each k are:
- For k=2, X=4
- For k=3, X=6
- For k=4, X=8
- For k=5, X=10
- For k=6, X=12
- For k=7, X=14
- For k=8, X=16
- For k=9, X=18
- For k=10, X=20
- For k=11, X=22
- For k=12, X=24
The expected value E(X) is calculated as follows:
E(X)=∑(Xi⋅P(ki))
Plugging in the values:
E(X)=4⋅136+6⋅236+8⋅336+10⋅436+12⋅536+14⋅636+16⋅536+18⋅436+20⋅336+22⋅236+24⋅136
=436+1236+2436+4036+6036+8436+8036+7236+6036+4436+2436
=50436
Simplifying gives:
E(X)=14
The expected value of X is 14.
Similar Questions
An unbiased die is tossed 3 times, suppose that a variable x is assigned the value k, when k consecutive sixes are obtained for else x takes the value –1 . Then expected value of x is:
A. 182216
B. 172216
C. −182216
D. −172216
View SolutionLet a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.
View Solution
Knowledge Check
The probability distribution of the discrete random variable X is shown in the table below. What is the expected value of X?
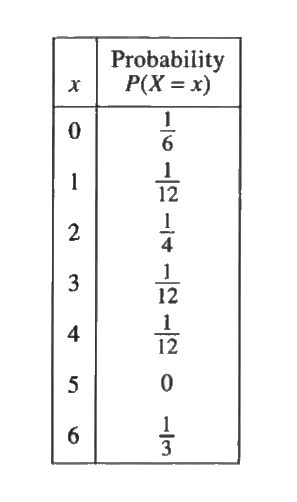 A16B13C1D316
A16B13C1D316
The probability of a random variable X is given below
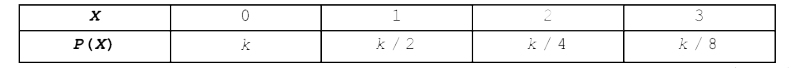
Determine the value of k
View SolutionA biased coin with probability of getting head is twice that of tail, is tossed 4 times If a random variable X is number of heads obtained, then expected value of X is :
View SolutionA biased coin with probability of getting head is twice that of tail, is tossed 4 times If a random variable X is number of heads obtained, then expected value of X is :
View SolutionA pair of fair dice is rolled at a time. The random variable X is the maximum of the two numbers shows on the dice. Find the probability distribution of X and mean of X.
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionIf the quadratic x2−2x+k=0 has equal roots, then value of k is ______.
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View Solution
