A hollow sphere of mass M and radius r is immersed in a tank of water (denstiy ρw). The sphere would float if it were set free. The sphere is tied to the bottom of the tank by two wires which makes angle 45∘ with the horizontal as shown in the figure. The tension T1 in the wire is :

43πR3ρwg−Mg√2
23πR3ρwg−Mg
43πR3ρwg−Mg2
43πR3ρwg=Mg
The correct Answer is:A
Step by step video & image solution for A hollow sphere of mass M and radius r is immersed in a tank of water (denstiy rho_(w)). The sphere would float if it were set free. The sphere is tied to the bottom of the tank by two wires which makes angle 45^(@) with the horizontal as shown in the figure. The tension T_(1) in the wire is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A hollow sphere of mass M=50kg and radius r=(340π)1/3m is immersed in a tank of water (density ρw=103kg/m3). The sphere is tied to the bottom of a tank by two wires A and B as shown. Tension in wire A is (g=10m/s2)
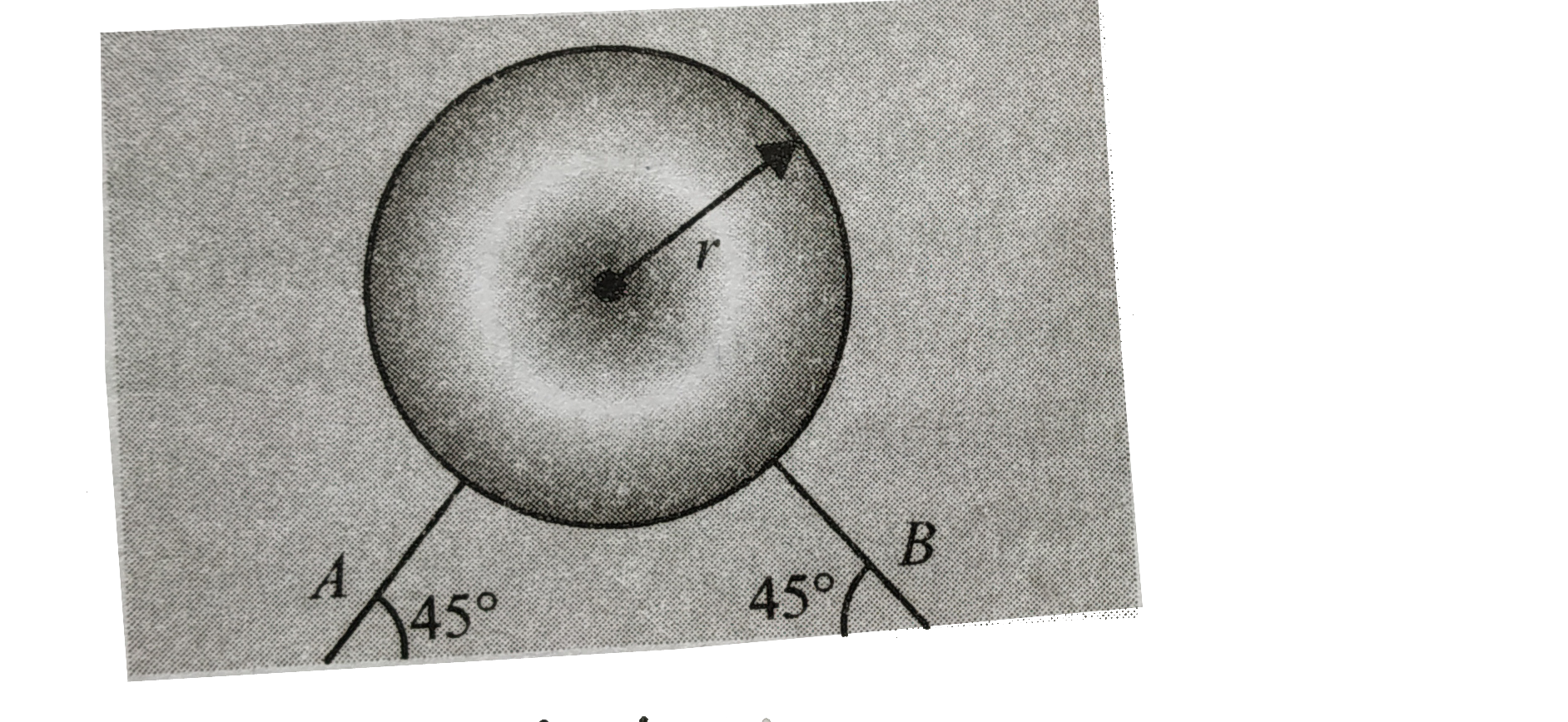
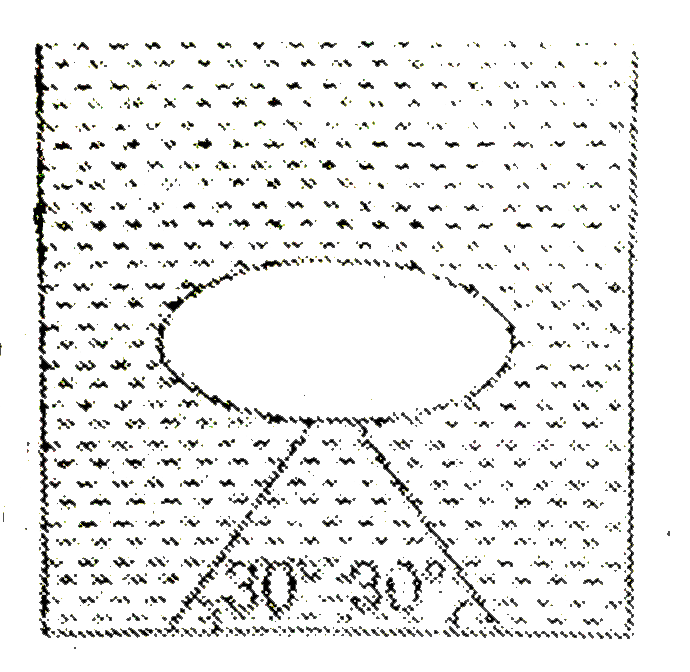
View SolutionA hollow object of volume V is immersed in a tank. The object is tied to the bottom of the tank by two wires which make an angle 30∘ with the horizontal as shown in figure. The object would float if it was set free and one forth volume is immersed in liquid of density ρ0. The tension in the wires is
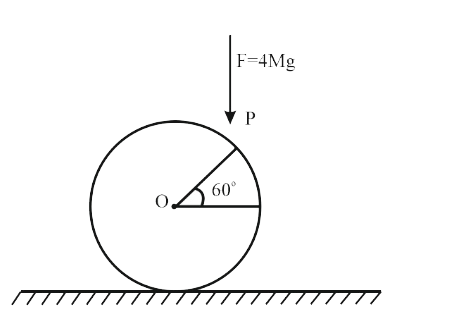
View SolutionA uniform solid sphere of mass M and radius R is lying on a rough horizonal plane. A constant force F=4Mg acts vertically downwards at point P such that the line OP makes an angle of 60∘ with the horizontal as shown in the figure. The minimum value of the coefficient of friction μ so that sphere performs pure rolling, is
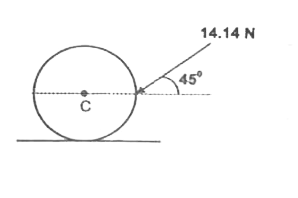
View SolutionA uniform sphere of mass 20kg and radius 10cm is placed on a rough horizontal surface . The coefficient of friction between the sphere and the surface is 0.5.If a force of magnitude 14.14 N is applied on the sphere at an angle of 45∘ with horizontal as shown in the figure, calculate
(a) frictional force
(b) acceleration of the sphere
(c ) angular acceleration of the sphere
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
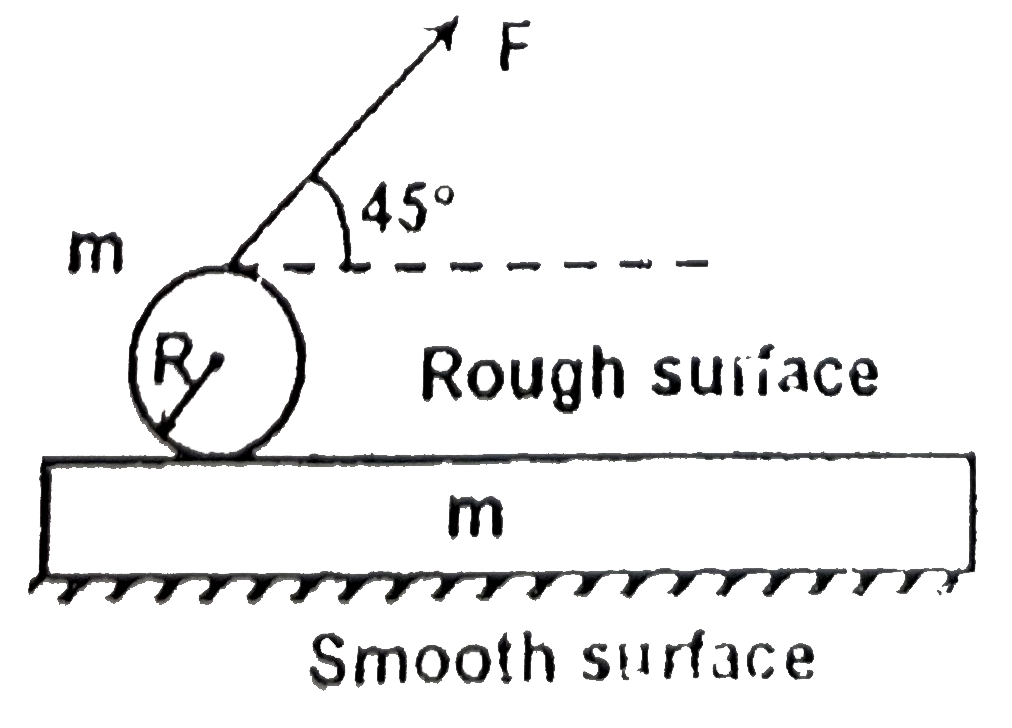
View SolutionA solid sphere of mass m and radius R is released from top of an incline having co-efficent of friction μ and making an angle of 45∘ with the horizontal. Choose the correct alternative (s)
View SolutionA hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Consider points A and B as shown in the figure.
View SolutionA hollow sphere is completely filled with a liquid having a density ρ. The radius of the sphere is R. Now the sphere is puloled with a constant horizontal acceleration of g on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Coordinate of the point having the maximum pressure is
View SolutionA sphere of mass 20 kg is suspended by a metal wire of unstretched length 4 m and diameter 1 mm. When in equilibrium there is a clear gap of 2 mm between the sphere and the floor. The sphere is gently pushed aside so that the wire makes an angle θ with the vertical and is released. Find the maximum value of θ so that the sphere does not rub the floor. young's modulus of the metal of the wire is 2.0×1011Nm−2. Make appropriate approximation.
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View Solution
