There are 7 distinguishable rings. The number of possible five - rings arrangements on the four fingers (except the thumb) of one hand (the order of the rings on each finger is to be counted and it is not required that each finger has a ring is equal to
214110
211410
124110
141120
The correct Answer is:D
To solve the problem of arranging 5 distinguishable rings on 4 fingers (excluding the thumb), we can break down the solution into clear steps.
1. Select 5 Rings from 7:
We need to choose 5 rings from a total of 7 distinguishable rings. The number of ways to choose 5 rings from 7 can be calculated using the combination formula:
Number of ways to choose 5 rings=(75)=7!5!(7−5)!=7!5!⋅2!
Simplifying this gives:
(75)=7×62×1=21
Hint: Use the combination formula (nr)=n!r!(n−r)! to find the number of ways to choose rings.
2. Arrange the 5 Rings on 4 Fingers:
Each of the 5 selected rings can be placed on any of the 4 fingers. Since the order of the rings on each finger matters, we calculate the number of arrangements as follows:
Number of arrangements=45
This is because each ring can independently be placed on any of the 4 fingers.
Hint: Remember that for each ring, you have multiple choices (in this case, 4 fingers).
3. Calculate the Total Arrangements:
Now, we multiply the number of ways to choose the rings by the number of arrangements:
Total arrangements=(75)×45=21×45
First, calculate 45:
45=1024
Now, multiply:
21×1024=21504
Hint: When multiplying large numbers, break them down into smaller parts if necessary to simplify calculations.
Final Answer:
The total number of possible arrangements of 5 rings on 4 fingers is 21504.
We need to choose 5 rings from a total of 7 distinguishable rings. The number of ways to choose 5 rings from 7 can be calculated using the combination formula:
Number of ways to choose 5 rings=(75)=7!5!(7−5)!=7!5!⋅2!
Simplifying this gives:
(75)=7×62×1=21
Each of the 5 selected rings can be placed on any of the 4 fingers. Since the order of the rings on each finger matters, we calculate the number of arrangements as follows:
Number of arrangements=45
This is because each ring can independently be placed on any of the 4 fingers.
Now, we multiply the number of ways to choose the rings by the number of arrangements:
Total arrangements=(75)×45=21×45
First, calculate 45:
45=1024
Now, multiply:
21×1024=21504
The total number of possible arrangements of 5 rings on 4 fingers is 21504.
Similar Questions
Knowledge Check
Cyclohexane exists its two chair conformations in rapid equilrium at room temperature.
Each carbon atom on a cyclohexane ring has one axial and one equatorial hydrogen. Ring-flipping converts axial II's to equatorial H's and vice-versa.

In substituted cyclohexane, groups larger than hydrogen are more stable in the equatorial position.
The cis isomer has two groups on the same side of the ring, either both up or both down.
The trans isomer has two groups on opposite side of the ring one up and one down.
Which of the following is most stable conformer of 1,2-dichlorocyclohexane?A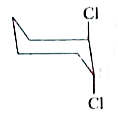 B
B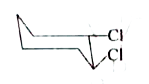 C
C DAll have equal stability
DAll have equal stabilityCyclonexane exists its two chair conformations in rapid equilrium at room temperature.
Each carbon atom on a cyclohexane ring has one axial and one equatorial hydrogen. Ring-flipping converts axial II's to equatorial H's and vice-versa.

In substituted cyclohexane, groups larger than hydrogen are more stable in the equatorial position.
The cis isomer has two groups on the same side of the ring, either both up or both down.
The trans isomer has two groups on opposite side of the ring one up and one down.
Find out most stable substituted cyclohexane among the following:A B
B C
C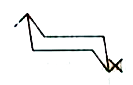 D
D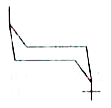
In how many ways three different rings can be worn in four fingers with at most one in each finger?
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be

View SolutionIn how many ways 6 rings of different types can be had in 4 given fingers of a hand?
View SolutionIn how many ways 5 rings of different types can be worn in 4 fingers?
View Solution
