If a new planet is discovered rotating around Sun with the orbital radius double that of earth, then what will be its time period (in earth's days)
The correct Answer is:1032
To find the time period of a new planet that is discovered rotating around the Sun with an orbital radius double that of Earth, we can use Kepler's Third Law of planetary motion. This law states that the square of the time period (T) of a planet is directly proportional to the cube of the semi-major axis (R) of its orbit.
1. Identify the known values:
- Let the orbital radius of Earth be R.
- The time period of Earth T is 365 days.
- The new planet has an orbital radius R′=2R.
2. Apply Kepler's Third Law:
- According to Kepler's Third Law:
T2∝R3
- For Earth:
T2=k⋅R3
- For the new planet:
T′2=k⋅(R′)3=k⋅(2R)3
3. Express T′ in terms of T:
- Substitute R′=2R into the equation:
T′2=k⋅(2R)3=k⋅8R3
- Since T2=k⋅R3, we can relate T′ and T:
T′2=8⋅T2
4. Take the square root:
- Taking the square root of both sides gives:
T′=√8⋅T
- Since √8=2√2, we have:
T′=2√2⋅T
5. Substitute the value of T:
- Substitute T=365 days:
T′=2√2⋅365
6. Calculate T′:
- Calculate 2√2:
2√2≈2⋅1.414≈2.828
- Therefore:
T′≈2.828⋅365≈1032.42 days
- Rounding gives approximately:
T′≈1032 days
Final Answer:
The time period of the new planet is approximately 1032 days.
- Let the orbital radius of Earth be R.
- The time period of Earth T is 365 days.
- The new planet has an orbital radius R′=2R.
- According to Kepler's Third Law:
T2∝R3
- For Earth:
T2=k⋅R3
- For the new planet:
T′2=k⋅(R′)3=k⋅(2R)3
- Substitute R′=2R into the equation:
T′2=k⋅(2R)3=k⋅8R3
- Since T2=k⋅R3, we can relate T′ and T:
T′2=8⋅T2
- Taking the square root of both sides gives:
T′=√8⋅T
- Since √8=2√2, we have:
T′=2√2⋅T
- Substitute T=365 days:
T′=2√2⋅365
- Calculate 2√2:
2√2≈2⋅1.414≈2.828
- Therefore:
T′≈2.828⋅365≈1032.42 days
- Rounding gives approximately:
T′≈1032 days
The time period of the new planet is approximately 1032 days.
Similar Questions
Knowledge Check
Assuming that earth and mars move in circular orbits around the sun, with the martian orbit being 1.52 times the orbital radius of the earth. The length of the martian year is days is
A(1.52)2/3×365B(1.52)3/2×365C(1.52)2×365D(1.52)3×365
The Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
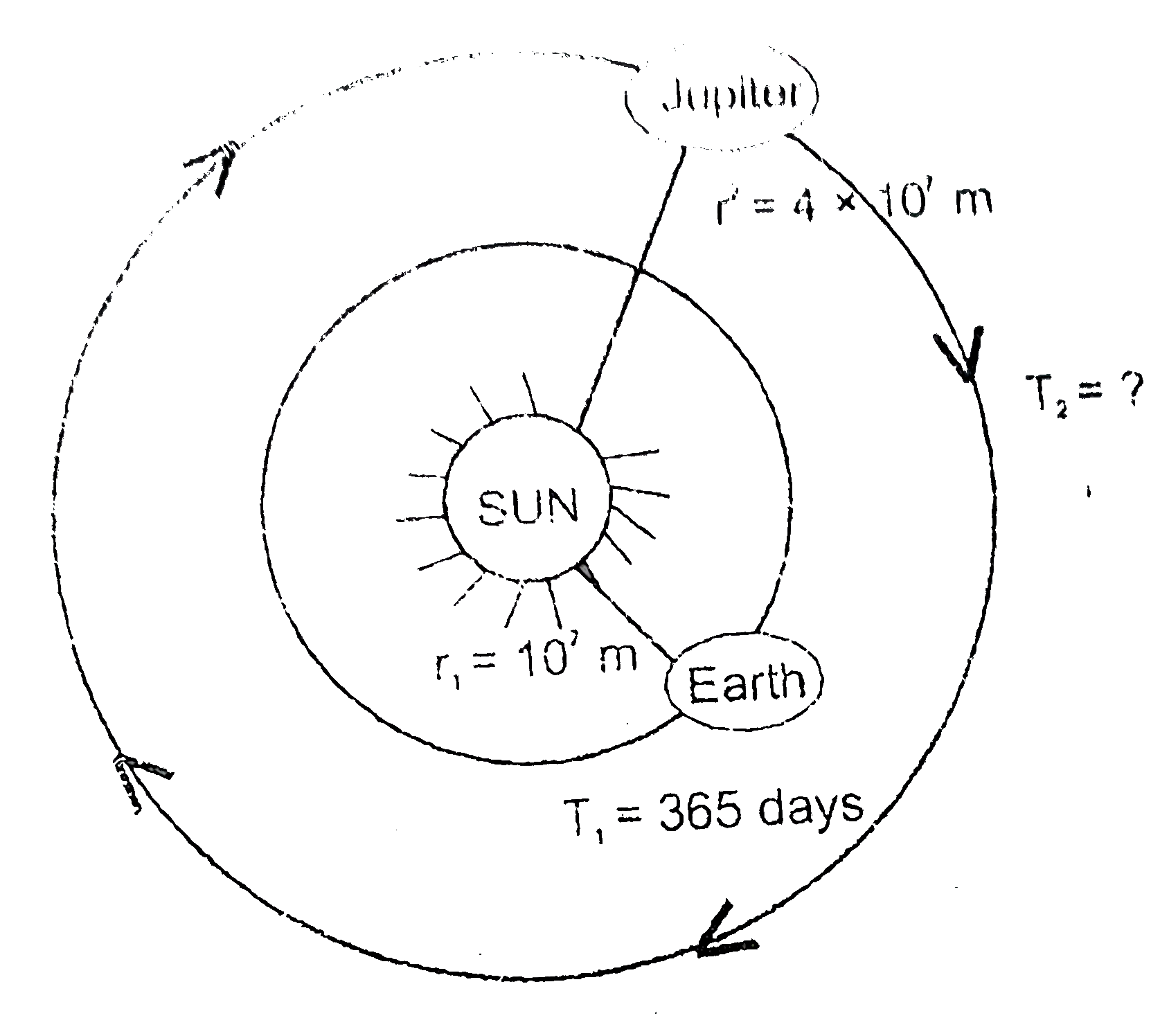 .
.
View SolutionIf the density of the planet is double that of the earth and the radius 1.5 times that of the earth, the acceleration due to gravity on the planet is
View SolutionIf the kinetic energy of a satellite orbiting around the earth is doubled then
View SolutionThe time period of a satellite of the earth is 10 hours. If the separations between the earth and the satellite is increased to 4 times the previous value, then what will be the new time period of the satellite ?
View SolutionSatellite is revolving around earth. If it's radius of orbit is increased to 4 times of the radius of geostationary statellite, what will become its time period ?
View SolutionA satellite having time period same as that of the earth's rotation about its own axis is orbiting the earth at a height 8R above the surface of earth. Where R is radius of earth. What will be the time period of another satellite at a height 3.5 R from the surface of earth ?
View SolutionIf earth radius reduces to half of its present value then the time period of rotation will become:
View Solution
