The period of oscillations of a magnet is 2 sec. When it is remagnetised so that the pole strength is 4 times its period will be
(a)1 sec
(b)2 sec
(c)4 sec
(d)8 sec
The correct Answer is:A
To solve the problem, we need to understand the relationship between the period of oscillation of a magnet and its pole strength.
1. Understand the Formula for Time Period (T):
The time period of oscillation (T) of a magnet is given by the formula:
T=2π√IM⋅B
where:
- I = moment of inertia,
- M = magnetic moment,
- B = magnetic field.
2. Relationship Between Time Period and Magnetic Moment:
The time period T is inversely proportional to the square root of the magnetic moment M:
T∝1√M
3. Expression for Magnetic Moment:
The magnetic moment M can be expressed in terms of pole strength m and length l:
M=m⋅l
Thus, if the pole strength is increased, the magnetic moment will also increase.
4. Change in Pole Strength:
If the pole strength becomes 4 times its original value, we can denote the new pole strength as:
m′=4m
5. New Magnetic Moment:
The new magnetic moment M′ will be:
M′=m′⋅l=4m⋅l=4M
6. New Time Period Calculation:
Since the time period is inversely proportional to the square root of the magnetic moment, we can write:
T′∝1√M′
Substituting M′=4M:
T′∝1√4M=12√M
7. Relating New Time Period to Original Time Period:
Since T∝1√M, we can express the new time period T′ in terms of the original time period T:
T′=T2
8. Substituting the Original Time Period:
Given that the original time period T is 2 seconds:
T′=2 seconds2=1 second
Conclusion:
The new period of oscillation when the pole strength is increased to 4 times its original value will be 1 second.
The time period of oscillation (T) of a magnet is given by the formula:
T=2π√IM⋅B
where:
- I = moment of inertia,
- M = magnetic moment,
- B = magnetic field.
The time period T is inversely proportional to the square root of the magnetic moment M:
T∝1√M
The magnetic moment M can be expressed in terms of pole strength m and length l:
M=m⋅l
Thus, if the pole strength is increased, the magnetic moment will also increase.
If the pole strength becomes 4 times its original value, we can denote the new pole strength as:
m′=4m
The new magnetic moment M′ will be:
M′=m′⋅l=4m⋅l=4M
Since the time period is inversely proportional to the square root of the magnetic moment, we can write:
T′∝1√M′
Substituting M′=4M:
T′∝1√4M=12√M
Since T∝1√M, we can express the new time period T′ in terms of the original time period T:
T′=T2
Given that the original time period T is 2 seconds:
T′=2 seconds2=1 second
The new period of oscillation when the pole strength is increased to 4 times its original value will be 1 second.
Similar Questions
Knowledge Check
Time period of oscillation of a spring is 12 s on earth. What shall be the time period if it is taken to moon?
A6 sB12 sC36 sD72 sThe time period of oscillation of a bar magnet suspended horizontaliy along the magnetic meridian is T0. If this magnet is replaced by another magnet of the same size and pole strength but with double the mass, the new time period will be
AT02BT0√2C√2T0D2T0
The time period of oscillation of the block as shown in figure is
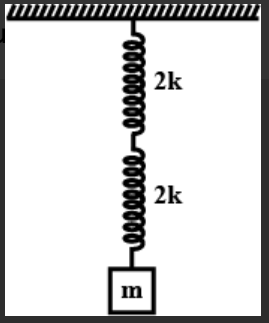
View SolutionThe time period of oscillations of a simple pendulum is 1 minute. If its length is increased b 44% then its new time period of oscillation will be
View SolutionThe time period of oscillation of a magnet in a vibration magnetometer is 1.5 seconds. The time period of oscillation of another of another magnet similar in size, shap and mass but having one-fourth magnetic moment than that of first magnet, oscillating at same place will be
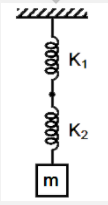
View SolutionTime period of oscillation for given combination will be :
View SolutionA deflection magnetometer is adjusted in the usual way . When a magnet is introduced , the deflection observed is θ=60∘ and the period of oscillation of the needle in magnetometer is T . When the magnet is removed the time period of oscillation is T0 . The relation between T and T0 is
View SolutionThe time period of oscillation of a simple pendulum is √2s. If its length is decreased to half of initial length, then its new period is
View Solution
_S01_040_Q01.png)