Total vapour pressure of mixture of 1 mol volatile component A(P∘A=100 mm Hg) and 3 mol of volatile component
B(P∘B=60 mm Hg) is 75 mm. For such case -
There is positive deviation from Raoult's law
Boiling point has been lowered
Force of attraction between A and B is smaller than that between A and A or between B and B.
All the above statements are correct
The correct Answer is:D
To solve the problem, we will use Raoult's Law and Dalton's Law of partial pressures. Here are the steps to find the total vapor pressure of the mixture and analyze the statements given.
Step 1: Identify the given data
- Moles of component A (volatile): nA=1
- Vapor pressure of pure component A: P0A=100mm Hg
- Moles of component B (volatile): nB=3
- Vapor pressure of pure component B: P0B=60mm Hg
- Total vapor pressure of the mixture: P=75mm Hg
Step 2: Calculate the total number of moles in the mixture
The total number of moles in the mixture is:
ntotal=nA+nB=1+3=4moles
Step 3: Calculate the mole fractions of components A and B
The mole fraction of component A (XA) and component B (XB) can be calculated as follows:
XA=nAntotal=14=0.25
XB=nBntotal=34=0.75
Step 4: Apply Raoult's Law to find the partial pressures
According to Raoult's Law, the partial pressures of components A and B are given by:
PA=P0A⋅XA=100mm Hg⋅0.25=25mm Hg
PB=P0B⋅XB=60mm Hg⋅0.75=45mm Hg
Step 5: Calculate the total vapor pressure of the mixture
The total vapor pressure P of the mixture is the sum of the partial pressures:
P=PA+PB=25mm Hg+45mm Hg=70mm Hg
Step 6: Compare the calculated total vapor pressure with the given total vapor pressure
The calculated total vapor pressure is 70mm Hg, which is less than the given total vapor pressure of 75mm Hg. This indicates a positive deviation from Raoult's Law.
Step 7: Analyze the statements
1. Positive deviation from Raoult's Law: Correct, as 70mm Hg<75mm Hg.
2. Boiling point has been lowered: Correct, since the vapor pressure is higher than expected, indicating a lower boiling point.
3. Force of attraction between AB smaller than between AA or BB: Correct, as the mixture exhibits positive deviation, indicating weaker interactions between A and B compared to A-A or B-B interactions.
Conclusion
All statements are correct, so the answer is that all of the above statements are true.
---
- Moles of component A (volatile): nA=1
- Vapor pressure of pure component A: P0A=100mm Hg
- Moles of component B (volatile): nB=3
- Vapor pressure of pure component B: P0B=60mm Hg
- Total vapor pressure of the mixture: P=75mm Hg
The total number of moles in the mixture is:
ntotal=nA+nB=1+3=4moles
The mole fraction of component A (XA) and component B (XB) can be calculated as follows:
XA=nAntotal=14=0.25
XB=nBntotal=34=0.75
According to Raoult's Law, the partial pressures of components A and B are given by:
PA=P0A⋅XA=100mm Hg⋅0.25=25mm Hg
PB=P0B⋅XB=60mm Hg⋅0.75=45mm Hg
The total vapor pressure P of the mixture is the sum of the partial pressures:
P=PA+PB=25mm Hg+45mm Hg=70mm Hg
The calculated total vapor pressure is 70mm Hg, which is less than the given total vapor pressure of 75mm Hg. This indicates a positive deviation from Raoult's Law.
1. Positive deviation from Raoult's Law: Correct, as 70mm Hg<75mm Hg.
2. Boiling point has been lowered: Correct, since the vapor pressure is higher than expected, indicating a lower boiling point.
3. Force of attraction between AB smaller than between AA or BB: Correct, as the mixture exhibits positive deviation, indicating weaker interactions between A and B compared to A-A or B-B interactions.
All statements are correct, so the answer is that all of the above statements are true.
Similar Questions
Answer the question (given below) which are based on the following diagra.
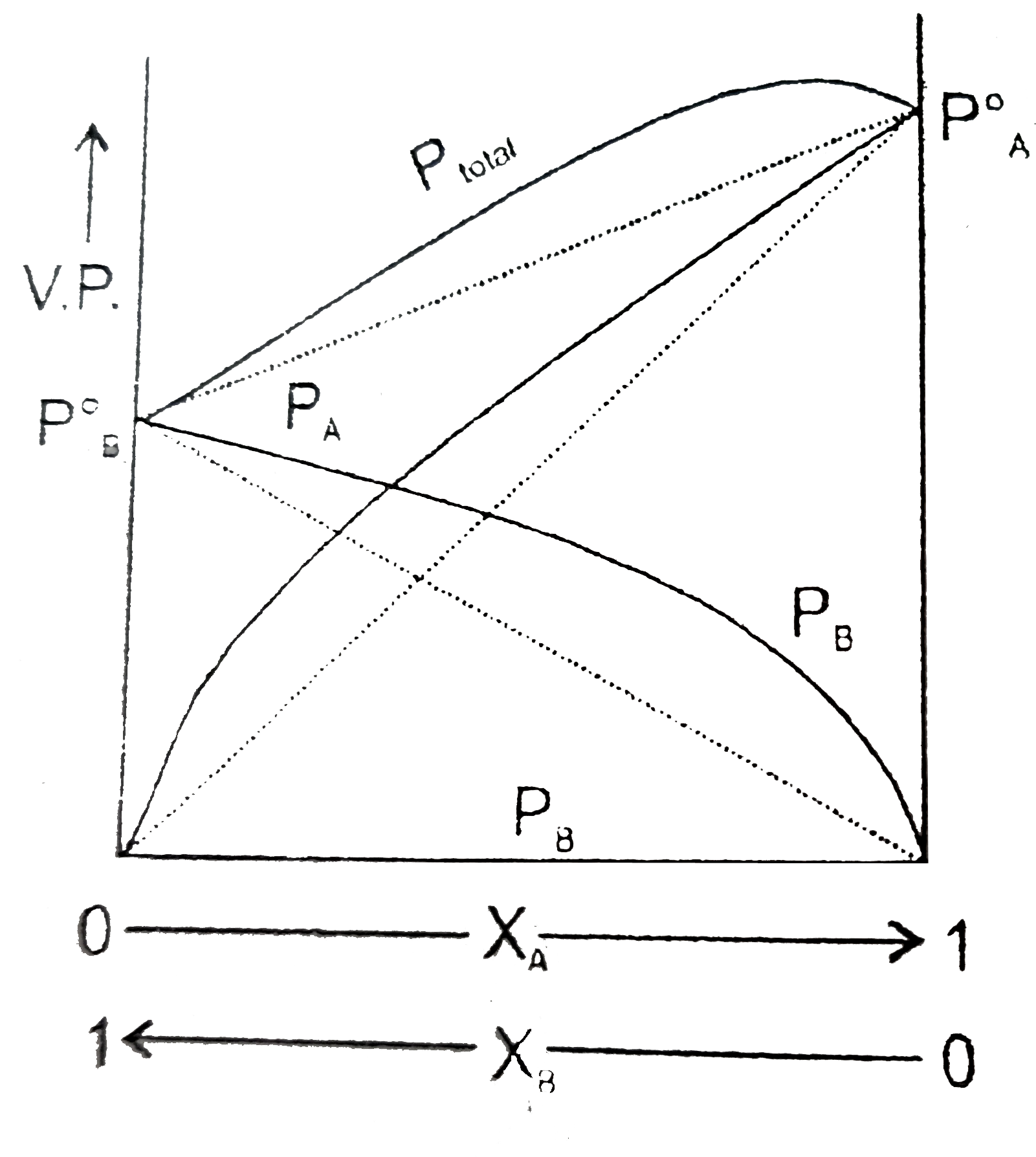
Consider some facts about the above phase diagram :
Vapour pressure diagram for real solutions of two liquids A and B that exhibit a positive deviation from Raoult's law. The vapour pressure of both A and B are greater than predicted by Raoult's law. The dashed lines lines represented the plots for ideal solutions.
Total vapour pressure of mixture of 1 mol of volatile component A(P∘A=100mmHg) and 3 mol of volatile component B(P∘B=60mmHg) is 75mm. For such case:
View SolutionTotal vapour pressure of mixture of 1 mol of volatile component A(PA∘=100mmHg) and 3 mol of volatile component B(PB∘=80mmHg is 75mm. For such case:
View SolutionTotal vapour pressure of mixture of 1 mole of volatile component A (P∘A=100mmHg) and 3 mole of volatile component B(P∘B=80mmHg) is 90mmHg. For such case :
View SolutionTotal vapour pressure of mixture of 1 mole of volaile components A (Pa%)=100 mm Hg) and 3 mole of volatile component B(P∘B=80mmHg) is 90 mm Hg. For such case:
View SolutionThe total vapour pressure of a mixture of 1 mole of A (PA=200mmHg) and 3 mole of B (PB=360 mm Hg) is 350 mm Hg. Then
View SolutionAt a given temperature total vapour pressure (in Torr) of a mixture of volatile components A and B is given by P=120−75XB hence vapour pressure of pure A and B respectively (in Torr) are
View SolutionThe vapour pressure at a given temperature of an ideal solution containing 0.2mol of non-volatile solute and 0.8mol of a solvent is 60mm of Hg. The vapour pressure of the pure solvent at the same temperature will be
View Solution1 mol benzene (P∘_(benzene)=42mm) and 2 mol toluence (P∘_(toluene)=36mm) will have
View SolutionThe vapour pressure of pure benzene at 25∘C is 640 mm Hg and that of the solute A in benzene is 630 mm of Hg. The molality of solution of
View SolutionThe total vapour pressure of a binary solution is gives by
P = (100XA+260XB)mm Hg
where,XAandXBare the molefractions of components A and B. This indicates that the:
View Solution
