Four wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
5Ω
10Ω
20Ω
54Ω
The correct Answer is:A
To find the equivalent resistance between the diagonally opposite corners of a square formed by four resistors of equal resistance (5 ohms each), we can follow these steps:
Step 1: Understand the Configuration
We have four resistors, each of 5 ohms, arranged in a square. Let's label the corners of the square as A, B, C, and D. We need to find the equivalent resistance between points B and D (the diagonally opposite corners).
Step 2: Identify the Paths
When looking for the equivalent resistance between B and D, we can see that there are two paths:
1. From B to A to D (through resistors R1 and R2).
2. From B to C to D (through resistors R3 and R4).
Step 3: Calculate the Resistance for Each Path
Each path consists of two resistors in series:
- For path B to A to D:
- R1 = 5 ohms (B to A)
- R2 = 5 ohms (A to D)
- Total resistance for this path (R_ABD) = R1 + R2 = 5 + 5 = 10 ohms.
- For path B to C to D:
- R3 = 5 ohms (B to C)
- R4 = 5 ohms (C to D)
- Total resistance for this path (R_BCD) = R3 + R4 = 5 + 5 = 10 ohms.
Step 4: Combine the Two Paths
Now, we have two resistances (10 ohms each) in parallel between points B and D. The formula for the equivalent resistance (R_eq) of two resistors in parallel (R1 and R2) is given by:
1Req=1R1+1R2
Substituting the values:
1Req=110+110
1Req=210=15
Step 5: Calculate the Equivalent Resistance
Taking the reciprocal gives us the equivalent resistance:
Req=5 ohms
Final Answer
The equivalent resistance between the diagonally opposite corners of the square is 5 ohms.
---
We have four resistors, each of 5 ohms, arranged in a square. Let's label the corners of the square as A, B, C, and D. We need to find the equivalent resistance between points B and D (the diagonally opposite corners).
When looking for the equivalent resistance between B and D, we can see that there are two paths:
1. From B to A to D (through resistors R1 and R2).
2. From B to C to D (through resistors R3 and R4).
Each path consists of two resistors in series:
- For path B to A to D:
- R1 = 5 ohms (B to A)
- R2 = 5 ohms (A to D)
- Total resistance for this path (R_ABD) = R1 + R2 = 5 + 5 = 10 ohms.
- R3 = 5 ohms (B to C)
- R4 = 5 ohms (C to D)
- Total resistance for this path (R_BCD) = R3 + R4 = 5 + 5 = 10 ohms.
Now, we have two resistances (10 ohms each) in parallel between points B and D. The formula for the equivalent resistance (R_eq) of two resistors in parallel (R1 and R2) is given by:
Taking the reciprocal gives us the equivalent resistance:
The equivalent resistance between the diagonally opposite corners of the square is 5 ohms.
Similar Questions
Knowledge Check
Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
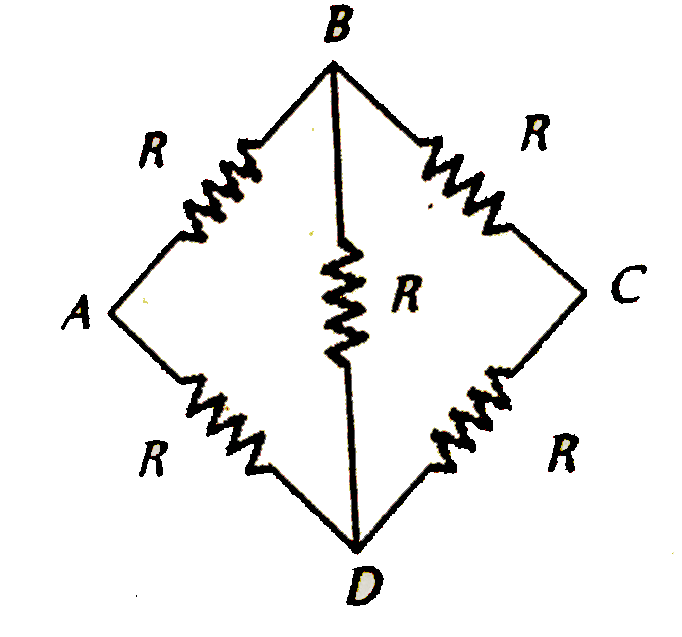 A12RB2RC58RD85R
A12RB2RC58RD85R
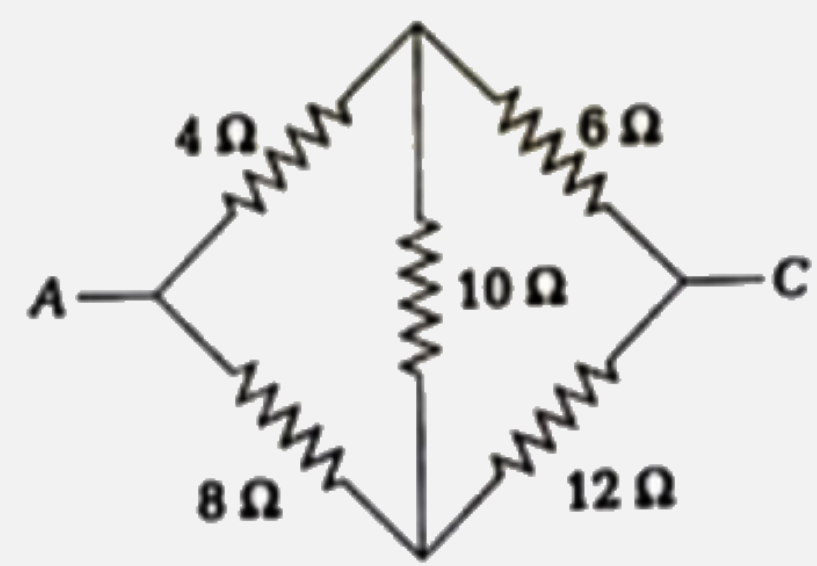
Seven resistance are connected as shown in the firgure. The equivalent resistance between A and B is approximately
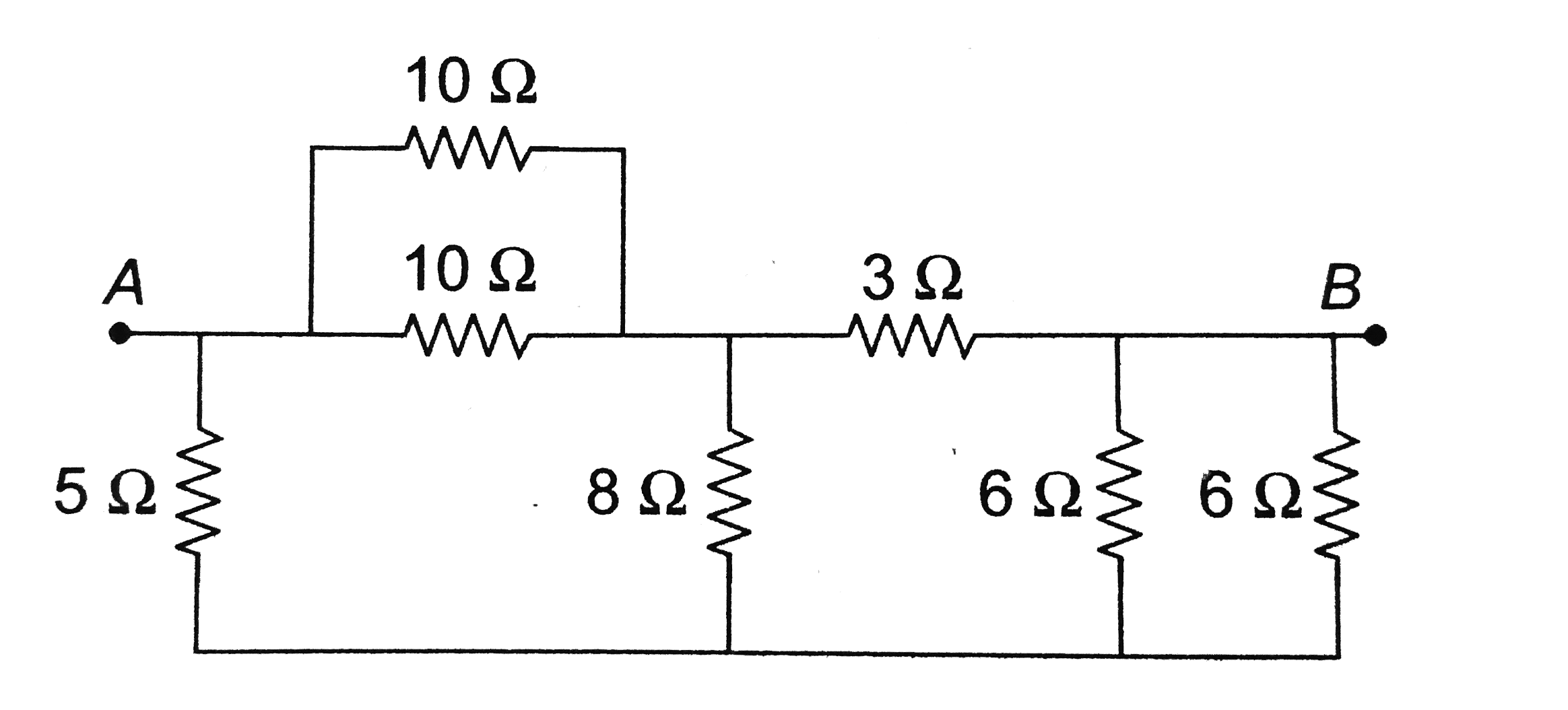
View SolutionEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
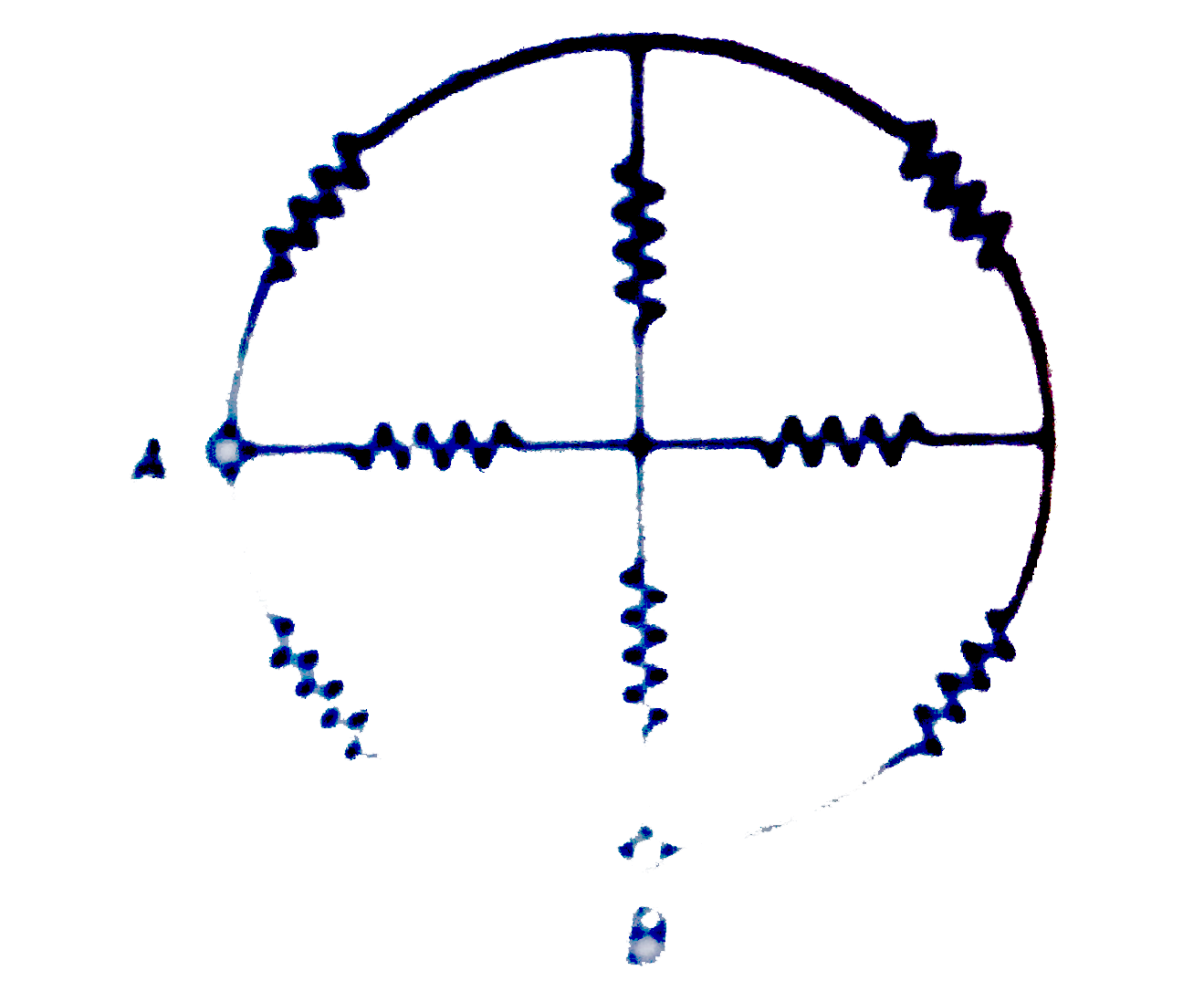
View SolutionSix equal resistance,eacch of resistance R are connected as shown in the figure.Equivalent resistance between P and Q is
_PHY_E05_276_Q01.png)
View SolutionFour equal resistors, each of resistance 10Ω, are connected as shown in the circuit diagram. The equivalent resistance between A and B is
View SolutionTwelve resistors of equal value R are connected in the form of a cube. Effective resistance between diagonals of the cube is

View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View SolutionSix resistors each of 10 ohm are connected shown. The equivalent resistance between points X and Y is
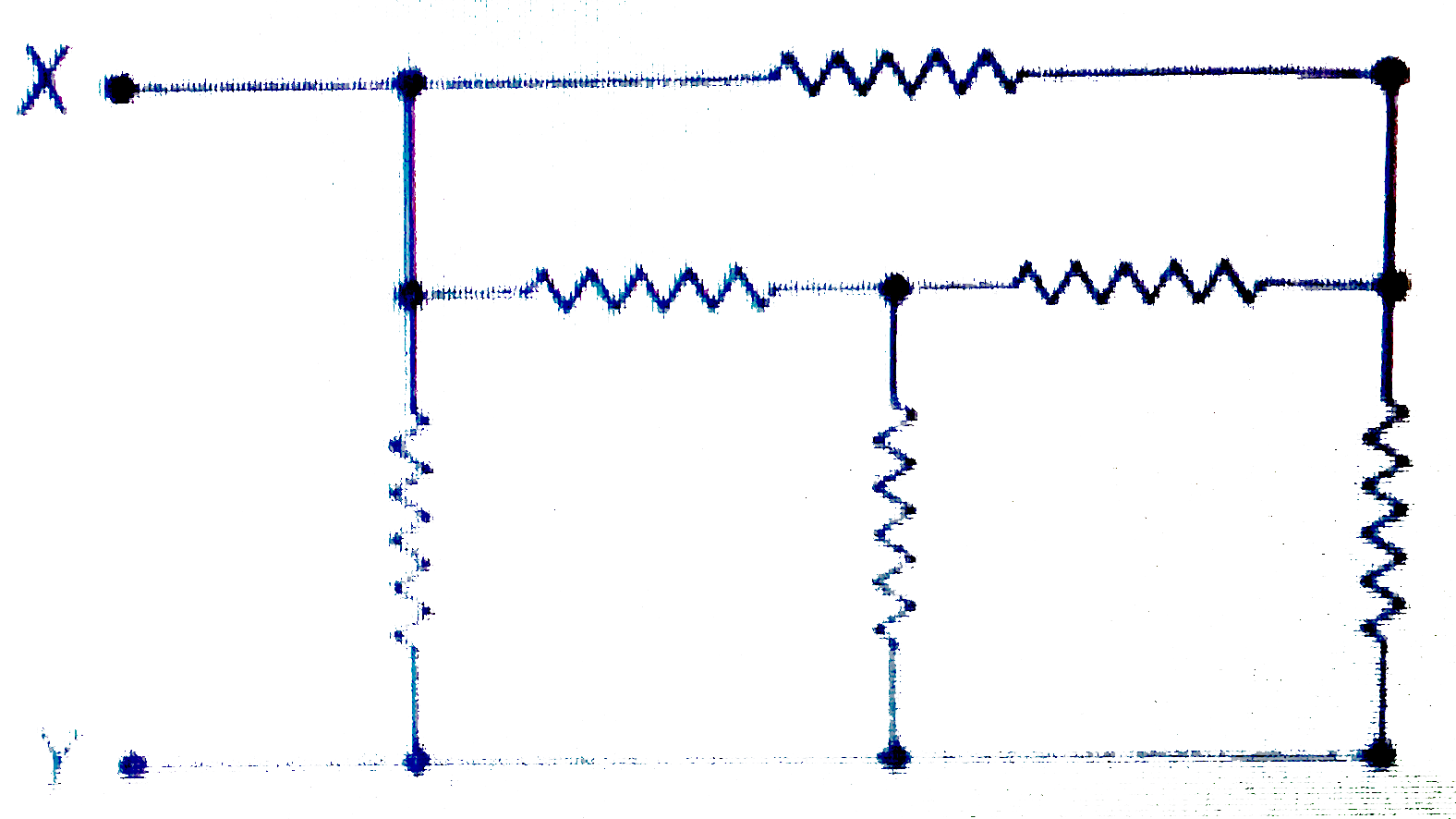
View Solution