When a polaroid sheet is rotated between two crossed polaroids, the intensity of the transmitted will be maximum, when angle θ between pass axes is
θ=90∘
θ=0∘
θ=45∘
it is independent of angle
The correct Answer is:C
To solve the problem of finding the angle θ at which the intensity of transmitted light is maximum when a polaroid sheet is rotated between two crossed polaroids, we can follow these steps:
1. Understanding the Setup:
We have two crossed polaroids (let's call them P1 and P2) that are oriented at an angle of 90∘ to each other. We introduce a third polaroid P0 that is rotated at an angle θ with respect to P1.
2. Applying Malus's Law:
According to Malus's law, the intensity of light transmitted through a polaroid is given by:
I=I0cos2(ϕ)
where I0 is the intensity of the incoming light and ϕ is the angle between the light's polarization direction and the polaroid's transmission axis.
3. Calculating Intensity After First Polaroid:
The intensity of light after passing through P1 is:
I1=I0cos2(0)=I0
(since the light is initially polarized along the axis of P1).
4. Intensity After the Third Polaroid:
The intensity after passing through the third polaroid P0 is:
I2=I1cos2(θ)=I0cos2(θ)
5. Intensity After the Second Polaroid:
The angle between P0 and P2 is 90∘−θ. Thus, the intensity after passing through P2 is:
I3=I2cos2(90∘−θ)=I0cos2(θ)sin2(θ)
6. Simplifying the Expression:
We can express I3 as:
I3=I0cos2(θ)sin2(θ)
Using the identity sin(2θ)=2sin(θ)cos(θ), we can rewrite this as:
I3=I04sin2(2θ)
7. Finding Maximum Intensity:
The maximum value of sin2(2θ) is 1, which occurs when 2θ=90∘ or θ=45∘.
8. Conclusion:
Therefore, the angle θ at which the intensity of the transmitted light is maximum is:
θ=45∘
Final Answer:
The angle θ between the pass axes for maximum transmitted intensity is 45∘.
---
We have two crossed polaroids (let's call them P1 and P2) that are oriented at an angle of 90∘ to each other. We introduce a third polaroid P0 that is rotated at an angle θ with respect to P1.
According to Malus's law, the intensity of light transmitted through a polaroid is given by:
I=I0cos2(ϕ)
where I0 is the intensity of the incoming light and ϕ is the angle between the light's polarization direction and the polaroid's transmission axis.
The intensity of light after passing through P1 is:
I1=I0cos2(0)=I0
(since the light is initially polarized along the axis of P1).
The intensity after passing through the third polaroid P0 is:
I2=I1cos2(θ)=I0cos2(θ)
The angle between P0 and P2 is 90∘−θ. Thus, the intensity after passing through P2 is:
I3=I2cos2(90∘−θ)=I0cos2(θ)sin2(θ)
We can express I3 as:
I3=I0cos2(θ)sin2(θ)
Using the identity sin(2θ)=2sin(θ)cos(θ), we can rewrite this as:
I3=I04sin2(2θ)
The maximum value of sin2(2θ) is 1, which occurs when 2θ=90∘ or θ=45∘.
Therefore, the angle θ at which the intensity of the transmitted light is maximum is:
θ=45∘
The angle θ between the pass axes for maximum transmitted intensity is 45∘.
Similar Questions
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids?
View SolutionDefine the term 'linearly polarised light'.
When does the intensity of transmitted light become maximum, when a polaroid sheet is rotated between two crossed polaroids ?
View SolutionA polaroid sheet is rotated in between two crossed polaroids P1andP2 At what θ of pass axis of polaroid sheet with pass-axis of polaroid P1 must be kept so that the final intensity of transmitted light be maximum? (P = polaroid sheet axis)
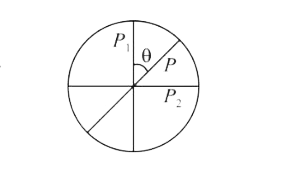
View SolutionA polaroid sheet is rotated in between two crossed polaroids P1andP2 At what θ of pass axis of polaroid sheet with pass-axis of polaroid P1 must be kept so that the final intensity of transmitted light be maximum? (P = polaroid sheet axis)

View Solution(a) Explain, using a suitable diagram, how unpolarized light gets linearly polarized by scattering.
(b) Describe briefly the variation of the intensity of transmitted light when a polaroid sheet kept between two crossed polaroids is rotated. Draw the graph depicting the variation of intensity with the angle of rotation. How many maxima and minima would be observed when θ vaeries from 0 to π ?
View SolutionAn unpolarised light of intensity 64 Wm^(-2) passes through three polarisers such that the transmission axis of the last polariser is normal to first. If the intensity of emerging light is 6 Wm(-2),then angle between first two polariser may be
View SolutionTwo polarising plates have polarising directions parallel score to trasmit maxmum intensity of light through what angle most either plate be turned in the intensites of the transmitted beam is to drop by half?
View Solution(a) What is linearly polarized light ? Describe briefly using a diagram how sunlight is polarised.
(b) Unpolarised light is incident on a polaroid. How would the intensity of transmitted light change when the polaroid is rotated?
View SolutionAn unpolarized light with intensity 2I0 is passed through a polaroid. The resultant intensity of the transmitted light will be
View SolutionUnpolarised light of intensity 32Wm−2 passes through three polarisers such that the transmission axis of the last polariser is crossed with first. If the intensity of the emerging light is 3Wm−2, the angle between the axes of the first two polarisers is
View Solution
