The distance between the centres of carbon and oxygen atoms in the carbon monoxide molecule is 1.130Å . Locate the centre of mass of the molecule relative to the carbon atom .
5.428Å
1.130Å
0.6457Å
0.3260Å
The correct Answer is:C
To locate the center of mass of the carbon monoxide (CO) molecule relative to the carbon atom, we can follow these steps:
Step 1: Understand the system
We have a carbon atom (C) and an oxygen atom (O) separated by a distance of 1.130 Å (angstroms). The atomic masses are:
- Mass of Carbon (m_C) = 12 u (atomic mass units)
- Mass of Oxygen (m_O) = 16 u
Step 2: Define the distance
Let the distance between the carbon and oxygen atoms be denoted as d=1.130Å=1.130×10−10m.
Step 3: Use the center of mass formula
The center of mass (CM) for two point masses can be calculated using the formula:
xCM=mC⋅xC+mO⋅xOmC+mO
Where:
- xC is the position of the carbon atom (we can set this as 0 for reference).
- xO is the position of the oxygen atom, which is d.
Step 4: Set the positions
- Let xC=0 (position of carbon).
- Therefore, xO=d=1.130×10−10m.
Step 5: Substitute the values into the formula
Substituting the known values into the center of mass formula:
xCM=(12u)⋅(0)+(16u)⋅(1.130×10−10m)12u+16u
This simplifies to:
xCM=0+18.08×10−1028u=18.08×10−1028
Step 6: Calculate the center of mass
Calculating the above expression:
xCM=18.08×10−1028≈0.6457×10−10m≈0.6457Å
Step 7: Conclusion
The center of mass of the CO molecule relative to the carbon atom is approximately 0.6457Å.
We have a carbon atom (C) and an oxygen atom (O) separated by a distance of 1.130 Å (angstroms). The atomic masses are:
- Mass of Carbon (m_C) = 12 u (atomic mass units)
- Mass of Oxygen (m_O) = 16 u
Let the distance between the carbon and oxygen atoms be denoted as d=1.130Å=1.130×10−10m.
The center of mass (CM) for two point masses can be calculated using the formula:
xCM=mC⋅xC+mO⋅xOmC+mO
Where:
- xC is the position of the carbon atom (we can set this as 0 for reference).
- xO is the position of the oxygen atom, which is d.
- Let xC=0 (position of carbon).
- Therefore, xO=d=1.130×10−10m.
Substituting the known values into the center of mass formula:
xCM=(12u)⋅(0)+(16u)⋅(1.130×10−10m)12u+16u
This simplifies to:
xCM=0+18.08×10−1028u=18.08×10−1028
Calculating the above expression:
xCM=18.08×10−1028≈0.6457×10−10m≈0.6457Å
The center of mass of the CO molecule relative to the carbon atom is approximately 0.6457Å.
Similar Questions
Which molecules have sp3 carbon atoms :
View SolutionThe distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is 1.1Å. Given, mass of carbon atom is 12 a.m.u. and mass of oxygen atom is 16 a.m.u., calculate the position of the centre of mass of the carbon monoxide molecule
View SolutionIn the formation of ethylene molecule , the carbon atom makes use of
View SolutionThe bond length between central carbon atom and other carbon atom is minimum in
View SolutionThe number of carbon atoms in a hydrogen carbonate radical is
View SolutionThe structure of a water molecule is shown in figure. Find the distance of the distance of the centre of mass of the molecule from the centre of the oxygen atom.
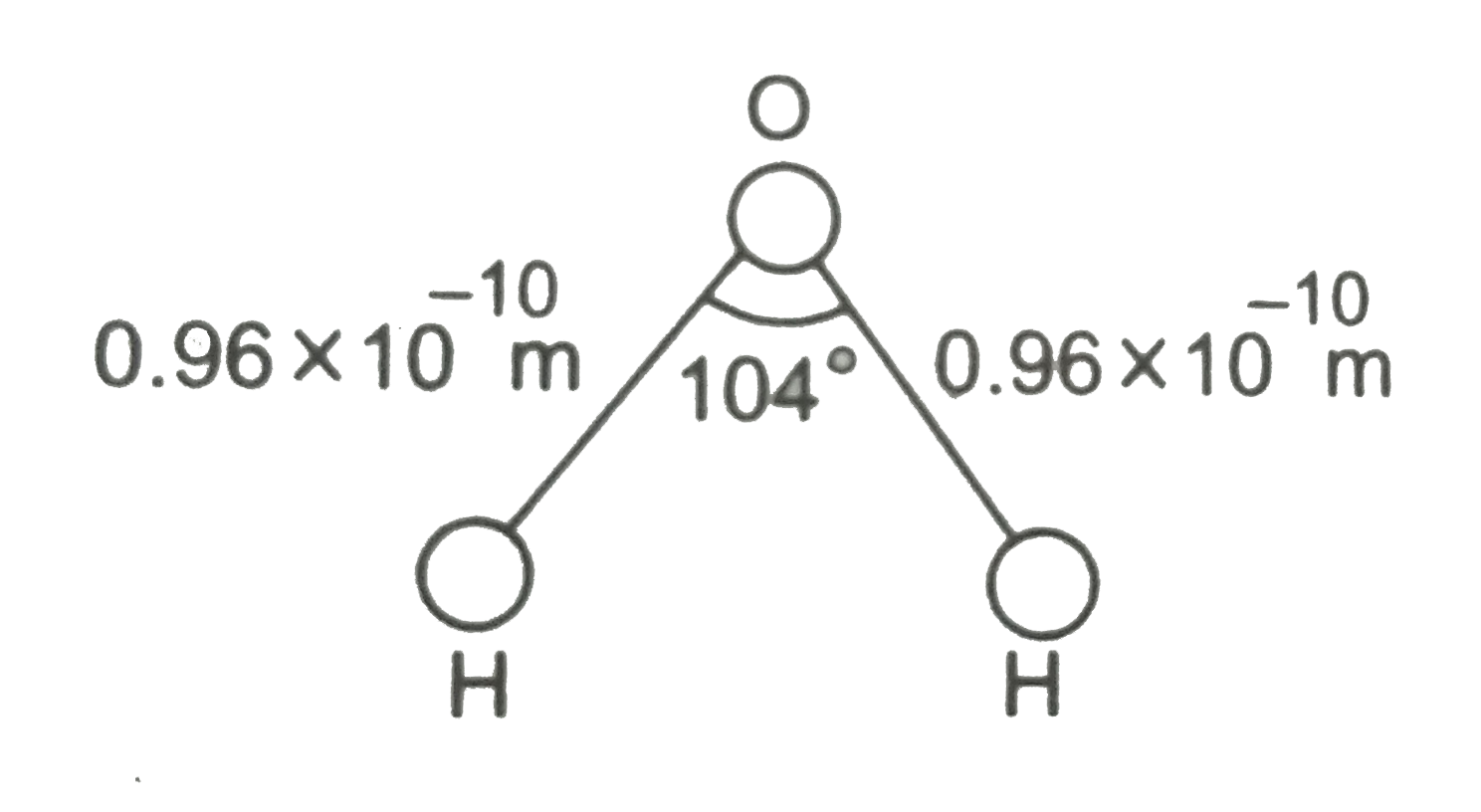
View SolutionWrite the name and structure of an alcohol with three carbon atoms in its molecule.
View SolutionIn a carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance 1.2×10−10m. The distance of the centre of mass from the carbon atom is
View SolutionIn acetylene molecule, the carbon atoms are linked by:
View SolutionIn a carbon monoxide molecule, the carbon and the oxygen atoms are separted by a distance 1.12×10−10 m. The distance of the centre of mass from the carbon atom is
A. 0.64×10−10m
B. 0.56×10−6m
C. 0.51×10−10m
D. 0.48×10−10 m
View Solution
