Two planets are at distance R1andR2 from the Sun. Their periods are T1andT2 then (T1T2)2 is equal to
R1R2
(R1R2)2
(R1R2)3
(R2R1)3
The correct Answer is:C
To solve the problem, we will use Kepler's Third Law of planetary motion, which states that the square of the period of orbit of a planet is directly proportional to the cube of the semi-major axis of its orbit.
1. Understanding the Relationship: According to Kepler's Third Law, we have the relationship:
T2∝R3
This means that for two planets orbiting the Sun at distances R1 and R2 with periods T1 and T2, we can write:
T21R31=T22R32
2. Rearranging the Equation: From the above relationship, we can rearrange to express the ratio of the squares of the periods:
T21T22=R31R32
3. Taking the Square Root: To find the ratio of the periods, we take the square root of both sides:
(T1T2)2=R31R32
4. Final Expression: Therefore, we can express the ratio of the squares of the periods in terms of the distances:
(T1T2)2=R31R32
Conclusion:
Thus, the final answer is:
(T1T2)2=R31R32
T2∝R3
This means that for two planets orbiting the Sun at distances R1 and R2 with periods T1 and T2, we can write:
T21R31=T22R32
T21T22=R31R32
(T1T2)2=R31R32
(T1T2)2=R31R32
Thus, the final answer is:
(T1T2)2=R31R32
Similar Questions
A body is in SHM with period T when oscillated from a freely suspended spring. If this spring is cut in two parts of length ratio 1:3& again oscillated from the two the two parts separatedly, then the periods are T1&T2 then find T1/T2.
View SolutionFor a given velocity, a projectile has the same range R for two angles of projection. If t1 and t2 are the time of flight in the two cases, then t1⋅t2 is equal to
View SolutionTwo spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionA planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
View SolutionTwo satellites A and B of masses m1 and m2(m1=2m2) are moving in circular orbits of radii r1 and r2(r1=4r2), respectively, around the earth. If their periods are TA and TB, then the ratio TA/TB is
View SolutionThe figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
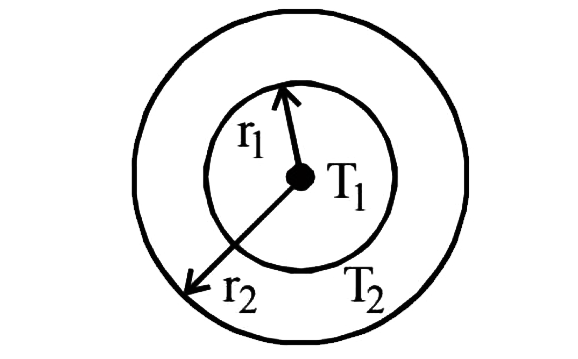
View SolutionABCD is a square with side AB = 2. A point P moves such that its distance from A equals its distance from the line BD. The locus of P meets the line AC at T1 and the line through A parallel to BD at T2 and T3. The area of the triangle T1T2T3 is :
View SolutionABCD is a square with side AB = 2. A point P moves such that its distance from A equals its distance from the line BD. The locus of P meets the line AC at T1 and the line through A parallel to BD at T2 and T3. The area of the triangle T1T2T3 is :
View SolutionTwo projectiles are thrown same speed in such a way that their ranges are equal. If the time of flights for the two projectiles are t1 and t2 the value of 't1t2' in terms of range 'R' and 'g' is
View SolutionTwo projectiles are thrown same speed in such a way that their ranges are equal. If the time of flights for the two projectiles are t1 and t2 the value of 't1t2' in terms of range 'R' and 'g' is
View Solution