A frog can be levitated in a magnetic field produced by a current in a vertical solenoid placed below the frog. This is possible because the body of the frog behaves as
paramagnetic
diamagnetic
ferromagnetic
anti - ferromagnetic
The correct Answer is:B
To solve the question, we need to understand the behavior of the frog in the magnetic field produced by the solenoid. Let's break down the solution step by step:
Step 1: Understanding the Scenario
A frog is placed above a vertical solenoid that generates a magnetic field when current flows through it. The question asks us to determine how the frog can be levitated in this magnetic field.
Hint: Consider the forces acting on the frog and the nature of the magnetic field produced by the solenoid.
Step 2: Analyzing Forces
For the frog to be levitated, the net force acting on it must be zero. The downward force acting on the frog is its weight (W). To achieve levitation, there must be an upward magnetic force (F_m) that counteracts the weight.
Hint: Think about how the magnetic force can act on the frog and what conditions are necessary for levitation.
Step 3: Magnetic Behavior of the Frog
The key to this phenomenon lies in the magnetic properties of the frog's body. The frog behaves as a diamagnetic substance. Diamagnetic materials are characterized by the fact that they are repelled by magnetic fields.
Hint: Recall the properties of diamagnetic materials and how they interact with magnetic fields.
Step 4: Interaction with the Magnetic Field
When the frog is placed above the solenoid, the magnetic field produced by the solenoid induces a magnetic response in the frog's body. The atoms in the frog's body behave like tiny magnets that align in opposition to the external magnetic field, resulting in a repulsive force.
Hint: Consider how the alignment of atomic magnetic moments in the frog contributes to the overall magnetic behavior.
Step 5: Conclusion
Since the frog is repelled by the magnetic field generated by the solenoid, the upward magnetic force can balance the downward gravitational force (weight), allowing the frog to levitate. Thus, we conclude that the body of the frog behaves as a diamagnetic substance.
Final Answer: The body of the frog behaves as a diamagnetic substance.
A frog is placed above a vertical solenoid that generates a magnetic field when current flows through it. The question asks us to determine how the frog can be levitated in this magnetic field.
For the frog to be levitated, the net force acting on it must be zero. The downward force acting on the frog is its weight (W). To achieve levitation, there must be an upward magnetic force (F_m) that counteracts the weight.
The key to this phenomenon lies in the magnetic properties of the frog's body. The frog behaves as a diamagnetic substance. Diamagnetic materials are characterized by the fact that they are repelled by magnetic fields.
When the frog is placed above the solenoid, the magnetic field produced by the solenoid induces a magnetic response in the frog's body. The atoms in the frog's body behave like tiny magnets that align in opposition to the external magnetic field, resulting in a repulsive force.
Since the frog is repelled by the magnetic field generated by the solenoid, the upward magnetic force can balance the downward gravitational force (weight), allowing the frog to levitate. Thus, we conclude that the body of the frog behaves as a diamagnetic substance.
Similar Questions
Knowledge Check
A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because
Athe magnetic field is constant.Bthe magnetic field is in the same plane as the cirular coil and it may or may not vary.Cthe magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably.Dboth (b) and (c)
Frogs are poikilothermic because body temperature
View SolutionA circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View SolutionChanging magnetic fields can set up current loops in nearby metal bodies and the currents are called as
View SolutionA thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as Bz=B0(1−αz) and Br=B0βr, where B0,α and β are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r0 and self inductance L. Assume the acceleration due to gravity as g.

Find the magnitude of current in the ring at a vertical position z.
View SolutionA thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as Bz=B0(1−αz) and Br=B0βr, where B0,α and β are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r0 and self inductance L. Assume the acceleration due to gravity as g.
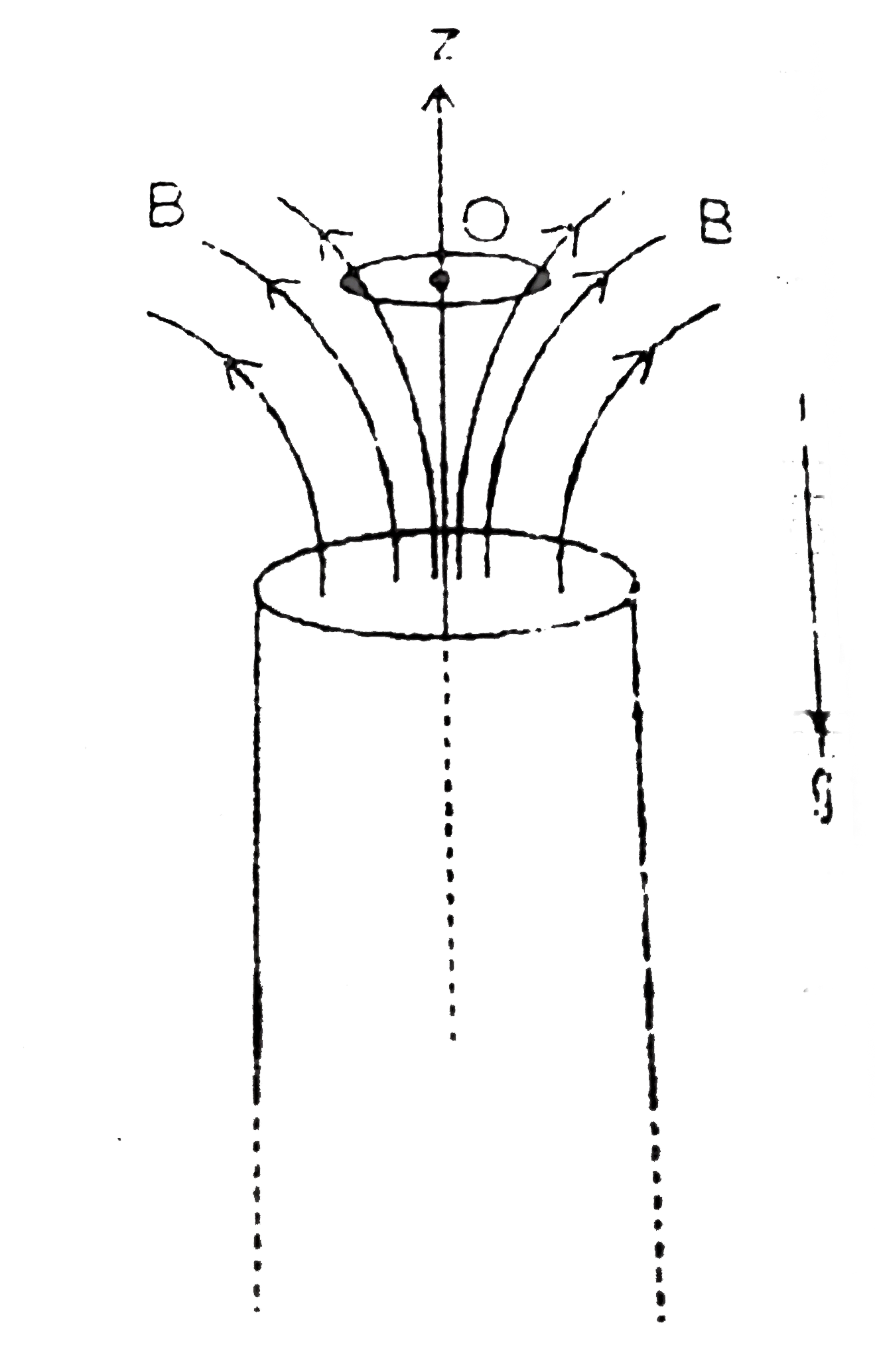
Find the vertical coordinates z for equilibrium position of the ring.
View SolutionA circular coil of radius 20cm and 20 turns of wire is mounted vertically with its plane in magnetic meridian.A small magnetic needle (free to rotate about vertical axis) is placed at the center of the coil.It is deflected through 45∘ when a current is passed through the coil and in equilbrium (Horizontal component of earth's field is 0.34×10−4T).The current in coil is:
View Solution
