A proton moving with a velocity of 0.125×105ms−1 Collides with a stationary helium atom. The velocity of the proton after the collision is
0.75×105ms−1
7.5×105ms−1
−0.75×105ms−1
0ms−1
The correct Answer is:C
To solve the problem of a proton colliding with a stationary helium atom, we will use the principles of conservation of momentum and the properties of elastic collisions.
1. Identify the masses and initial velocities:
- Mass of the proton, mp=1amu
- Mass of the helium atom, mHe=4amu
- Initial velocity of the proton, v0=0.125×105m/s
- Initial velocity of the helium atom, vHe0=0m/s
2. Set up the equations for elastic collision:
- For elastic collisions, the following two equations hold:
- Conservation of momentum:
mpv0+mHevHe0=mpv1+mHev2
- Conservation of kinetic energy (which implies the velocity of separation equals the velocity of approach):
v2−v1=v0
3. Substituting known values:
- Since vHe0=0:
1⋅(0.125×105)+4⋅0=1⋅v1+4⋅v2
- This simplifies to:
0.125×105=v1+4v2(Equation 1)
4. Using the velocity of separation:
- From the velocity of separation equation:
v2−v1=0.125×105(Equation 2)
5. Solving the equations:
- Rearranging Equation 2 gives:
v2=v1+0.125×105
- Substitute v2 from Equation 2 into Equation 1:
0.125×105=v1+4(v1+0.125×105)
- Expanding this:
0.125×105=v1+4v1+0.5×105
- Combine like terms:
0.125×105=5v1+0.5×105
- Rearranging gives:
5v1=0.125×105−0.5×105
5v1=−0.375×105
- Therefore:
v1=−0.075×105m/s
Final Answer:
The velocity of the proton after the collision is:
v1=−0.075×105m/s=−7500m/s
- Mass of the proton, mp=1amu
- Mass of the helium atom, mHe=4amu
- Initial velocity of the proton, v0=0.125×105m/s
- Initial velocity of the helium atom, vHe0=0m/s
- For elastic collisions, the following two equations hold:
- Conservation of momentum:
mpv0+mHevHe0=mpv1+mHev2
- Conservation of kinetic energy (which implies the velocity of separation equals the velocity of approach):
v2−v1=v0
- Since vHe0=0:
1⋅(0.125×105)+4⋅0=1⋅v1+4⋅v2
- This simplifies to:
0.125×105=v1+4v2(Equation 1)
- From the velocity of separation equation:
v2−v1=0.125×105(Equation 2)
- Rearranging Equation 2 gives:
v2=v1+0.125×105
- Substitute v2 from Equation 2 into Equation 1:
0.125×105=v1+4(v1+0.125×105)
- Expanding this:
0.125×105=v1+4v1+0.5×105
- Combine like terms:
0.125×105=5v1+0.5×105
- Rearranging gives:
5v1=0.125×105−0.5×105
5v1=−0.375×105
- Therefore:
v1=−0.075×105m/s
The velocity of the proton after the collision is:
v1=−0.075×105m/s=−7500m/s
Similar Questions
A ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA ball of mass m1 is moving with velocity 3v. It collides head on elastically with a stationary ball of mass m2 . The velocity of both the balls become v after collision. Then the value of the ratio m2m1 is
View Solution
Knowledge Check
A ball weighing 4 kg and moving with velocity of 8 m/sec. Collides with a stationary ball of mass 12 kg. After the collision, the two balls move together. The final velocity is
A0B2 m/secC8 m/secD16 m/secTwo identical balls A and B moving with velocities + 0.5 m/s and −0.3.m/s respectively collide head-on elastically. The velocities of the ball A and B after collision will be respectively
A+0.5m/sand+0.3m/sB−0.3m/sand+0.5m/sC + 0.3 m//s and + 0.5 m//sD−0.5m/sand+0.3m/s
A small ball is projected horizontally between two large blocks. The ball is given a velocity Vms−1 and each of the large blocks move uniformly with a velocity of 2Vms−1. The ball collides elastically with the blocks. If the velocity of the blocks do not change due to the collision, then find out the velocity of the ball after the 2nd collision.
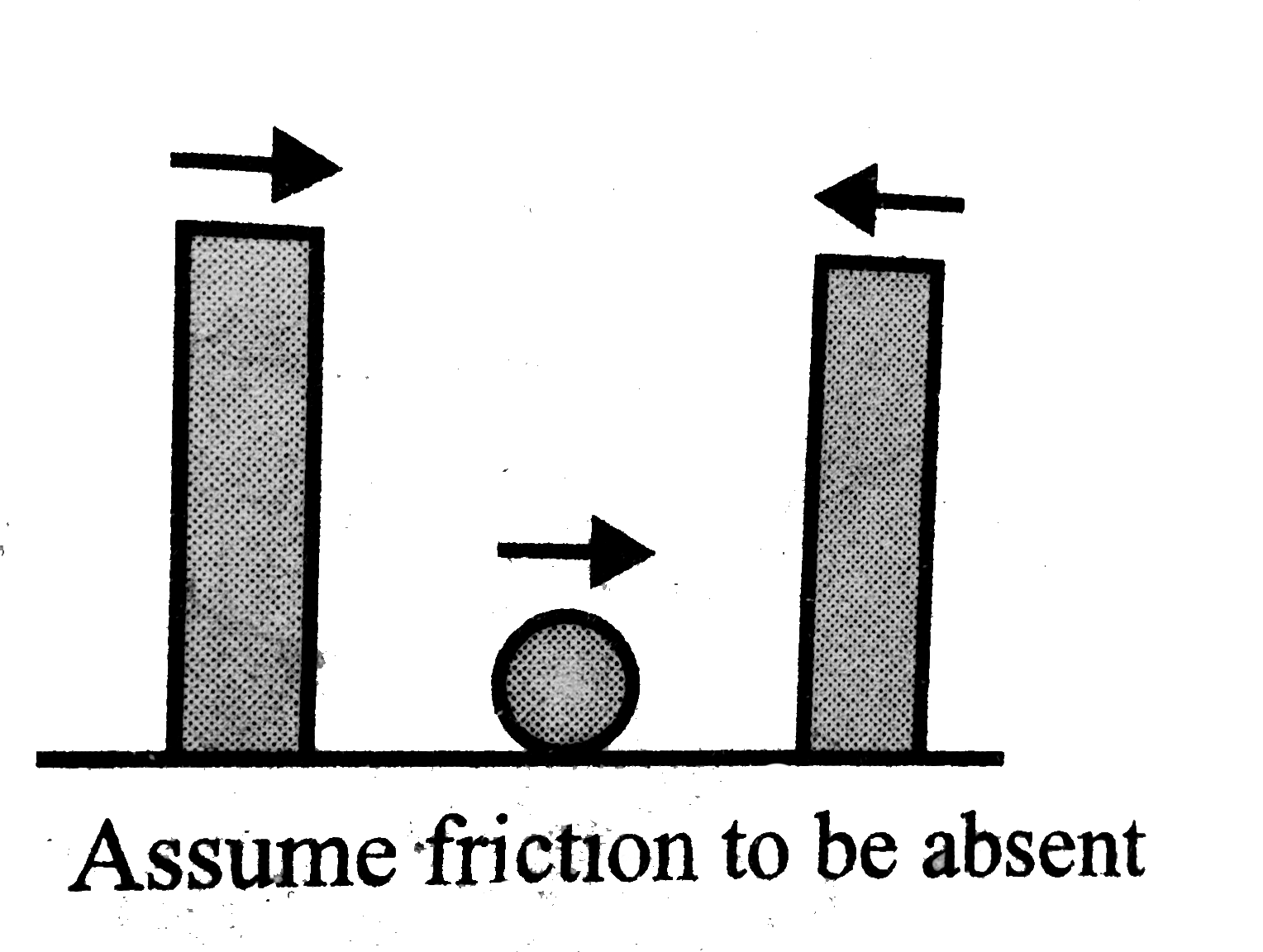
View SolutionTwo identical balls AandB having velocity of 0.5m/sand−0.3m/s respectively collide elastically in one dimension. The velocities of BandA after the collision respectively will be
View SolutionA ball moving with velocity 2ms−1 collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms−1) after collision will be
View SolutionA body starts moving with a velocity v0=10ms−1. It experiences a retardation equal to 0.2v2. Its velocity after 2s is given by
View SolutionA particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionA particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View Solution
