A uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will
be deflected to the left without increase in speed
be deflected to the right without increase in speed
not be deflected but its speed will decrease
not be deflected but its speed will increase
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the electron when it is projected in the presence of both electric and magnetic fields that are aligned in the same direction.
1. Understanding the Forces:
- The electron is negatively charged and is projected in the same direction as both the electric field (E) and the magnetic field (B).
- The force due to the electric field (F_E) acting on the electron can be calculated using the formula:
FE=qE
where q is the charge of the electron (which is negative).
2. Electric Force Direction:
- Since the charge of the electron is negative, the direction of the electric force will be opposite to the direction of the electric field. Therefore, if the electric field is directed to the right, the electric force will act to the left.
3. Magnetic Force Calculation:
- The magnetic force (F_B) acting on the electron can be calculated using the formula:
FB=q(v×B)
where v is the velocity of the electron and B is the magnetic field.
- Since the velocity of the electron is in the same direction as the magnetic field, the cross product v×B will be zero. Thus, the magnetic force acting on the electron is:
FB=0
4. Net Force on the Electron:
- The only force acting on the electron is the electric force, which is directed opposite to its motion. Therefore, the net force acting on the electron is:
Fnet=FE+FB=FE+0=FE
5. Effect on the Electron's Motion:
- Since the net force is acting in the opposite direction to the velocity of the electron, it will cause the electron to decelerate. The speed of the electron will decrease over time due to the electric force acting against its motion.
6. Conclusion:
- The electron will not be deflected because there is no magnetic force acting on it. Instead, it will experience a decrease in speed due to the electric force acting in the opposite direction.
Final Answer:
The electron will decelerate (its speed will decrease) but will not be deflected.
---
- The electron is negatively charged and is projected in the same direction as both the electric field (E) and the magnetic field (B).
- The force due to the electric field (F_E) acting on the electron can be calculated using the formula:
FE=qE
where q is the charge of the electron (which is negative).
- Since the charge of the electron is negative, the direction of the electric force will be opposite to the direction of the electric field. Therefore, if the electric field is directed to the right, the electric force will act to the left.
- The magnetic force (F_B) acting on the electron can be calculated using the formula:
FB=q(v×B)
where v is the velocity of the electron and B is the magnetic field.
- Since the velocity of the electron is in the same direction as the magnetic field, the cross product v×B will be zero. Thus, the magnetic force acting on the electron is:
FB=0
- The only force acting on the electron is the electric force, which is directed opposite to its motion. Therefore, the net force acting on the electron is:
Fnet=FE+FB=FE+0=FE
- Since the net force is acting in the opposite direction to the velocity of the electron, it will cause the electron to decelerate. The speed of the electron will decrease over time due to the electric force acting against its motion.
- The electron will not be deflected because there is no magnetic force acting on it. Instead, it will experience a decrease in speed due to the electric force acting in the opposite direction.
The electron will decelerate (its speed will decrease) but will not be deflected.
Similar Questions
A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View SolutionUniform electric and magnetic fields are produced in the same direction. An electron moves in such a way that its velocity remains in the direction of electric field. The electron will-
View SolutionIf an electron enters a magnetic field with its velocity pointing in the same direction as the magnetic field, then
View SolutionAn electron is fired parallel to uniform electric and uniform magnetic field acting simultaneously and in the same direction. The electron
View SolutionA uniform but increasing with time magnetic field exists in as cylindrical region. The direction of force on an electron at P as

View SolutionIn a region of space, a uniform magnetic field B exists in the x-direction. An electron is fired from the origin with its initial velocity u making an angle α with the y direction in the y-z plane. In the subsequent motion of the electron,

View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
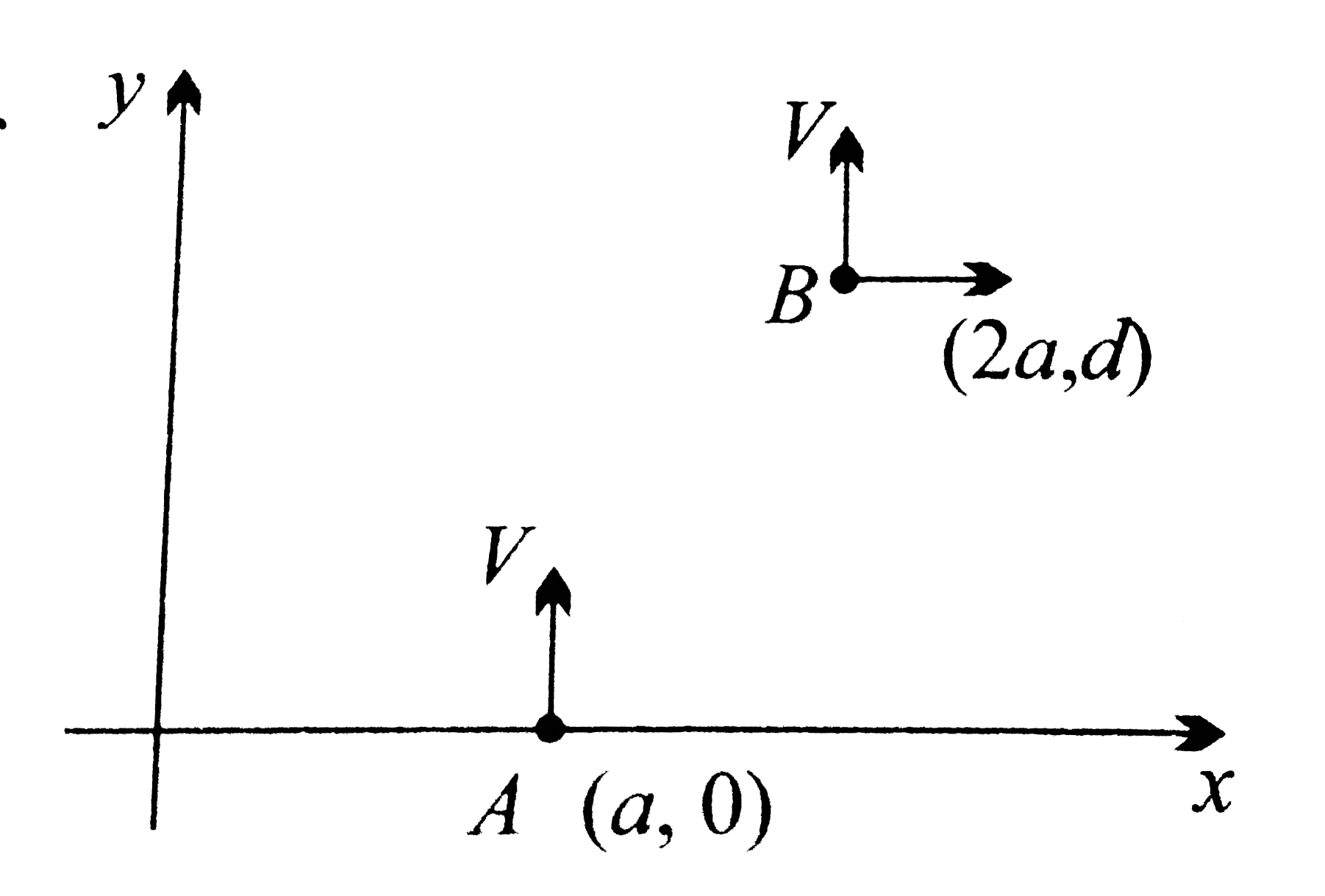 .
.
Find electric field.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
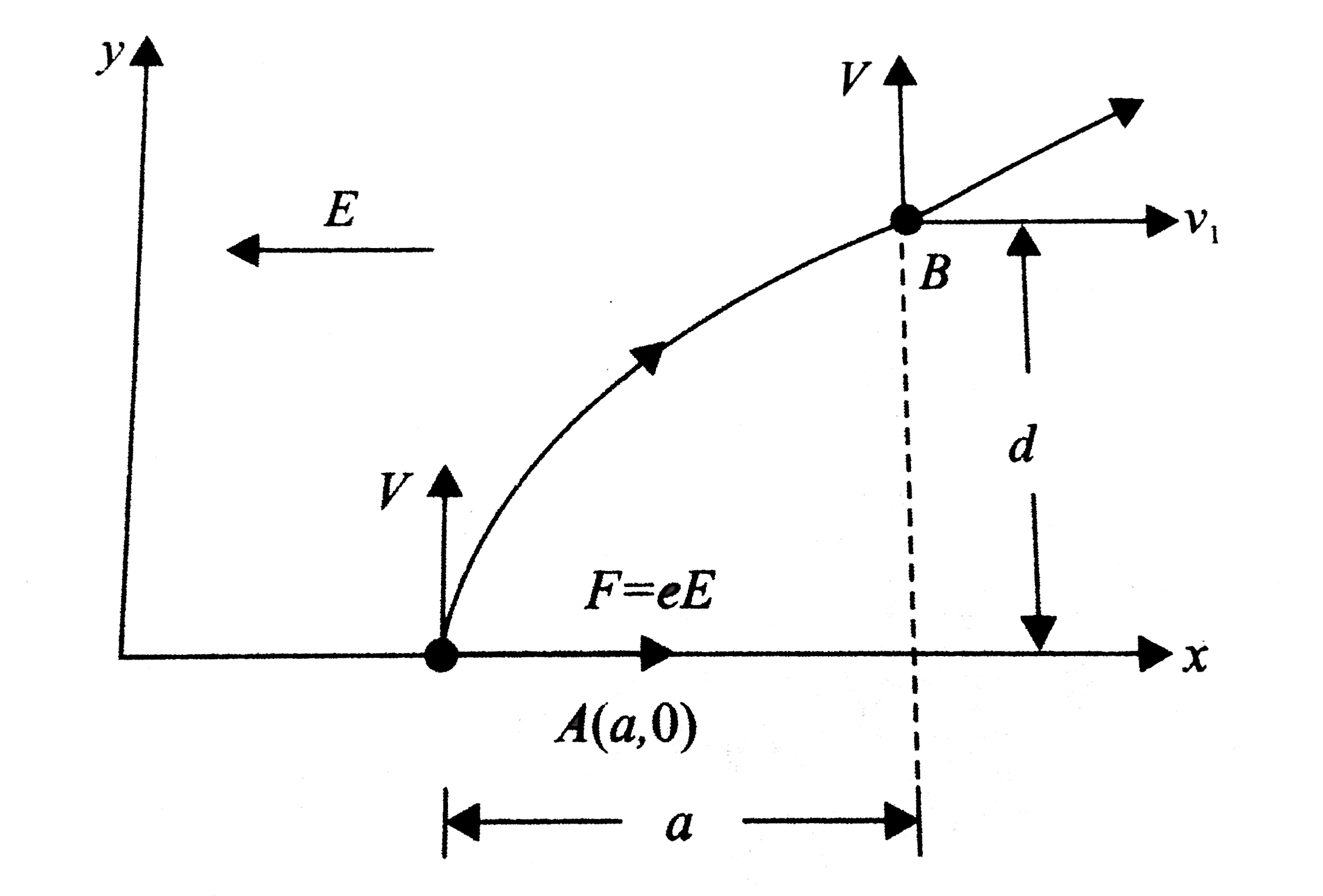 .
.
Find velocity at B.
View Solution