In an electrical cable there is a single wire of radius 9mm of copper. Its resistance is 5Ω. The cable is replaced by 6 different insulated copper, wires the radius of each wire is 3mm. Now the total resistance of the cable will be
7.5Ω
45Ω
90Ω
270Ω
The correct Answer is:A
To solve the problem, we need to find the total resistance of the cable when it is replaced by 6 different insulated copper wires, each with a radius of 3 mm.
1. Identify the Resistance Formula:
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity of the material, L is the length of the wire, and A is the cross-sectional area of the wire.
2. Calculate the Area of the Original Wire:
The radius of the original wire is R1=9mm=0.009m.
The cross-sectional area A1 of the original wire is:
A1=πR21=π(0.009)2=π×0.000081=0.000254469m2
3. Calculate the Resistance of the Original Wire:
Given that the resistance R1=5Ω, we can express it as:
R1=ρLA1
Rearranging gives:
ρL=R1A1=5×0.000254469=0.001272345Ohm m2
4. Calculate the Area of Each New Wire:
The radius of each new wire is r=3mm=0.003m.
The cross-sectional area A2 of each new wire is:
A2=πr2=π(0.003)2=π×0.000009=0.000028274m2
5. Calculate the Total Area of 6 Wires:
Since there are 6 wires, the total cross-sectional area Atotal is:
Atotal=6×A2=6×0.000028274=0.000169644m2
6. Calculate the Resistance of the New Configuration:
The resistance R2 of the new configuration can be expressed as:
R2=ρLAtotal
Substituting ρL from step 3:
R2=0.0012723450.000169644≈7.5Ω
Final Answer:
The total resistance of the cable when replaced by 6 different insulated copper wires is approximately 7.5Ω.
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity of the material, L is the length of the wire, and A is the cross-sectional area of the wire.
The radius of the original wire is R1=9mm=0.009m.
The cross-sectional area A1 of the original wire is:
A1=πR21=π(0.009)2=π×0.000081=0.000254469m2
Given that the resistance R1=5Ω, we can express it as:
R1=ρLA1
Rearranging gives:
ρL=R1A1=5×0.000254469=0.001272345Ohm m2
The radius of each new wire is r=3mm=0.003m.
The cross-sectional area A2 of each new wire is:
A2=πr2=π(0.003)2=π×0.000009=0.000028274m2
Since there are 6 wires, the total cross-sectional area Atotal is:
Atotal=6×A2=6×0.000028274=0.000169644m2
The resistance R2 of the new configuration can be expressed as:
R2=ρLAtotal
Substituting ρL from step 3:
R2=0.0012723450.000169644≈7.5Ω
The total resistance of the cable when replaced by 6 different insulated copper wires is approximately 7.5Ω.
Similar Questions
A 1m long wire of diameter 0.31mm has a resistance of 4.2Ω. If it is replaced by another wire of same material of length 1.5m and diameter 0.155mm, then the resistance of wire is
View SolutionThe resistance of a wire R Ω . The wire is stretched to double its length keeping volume constant. Now, the resistance of the wire will become
View SolutionWhen a wire is stretched and its radius becomes r/2 then its resistance will be
View SolutionA wire of resistance 4Ω is stretched to twice its original length. In the process of stretching, its area of cross-section gets halved. Now, the resistance of the wire is
View SolutionThe resistance of a wire is 10Ω. Its length is increased by 10% by stretching. The new resistance will now be
View SolutionIn a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
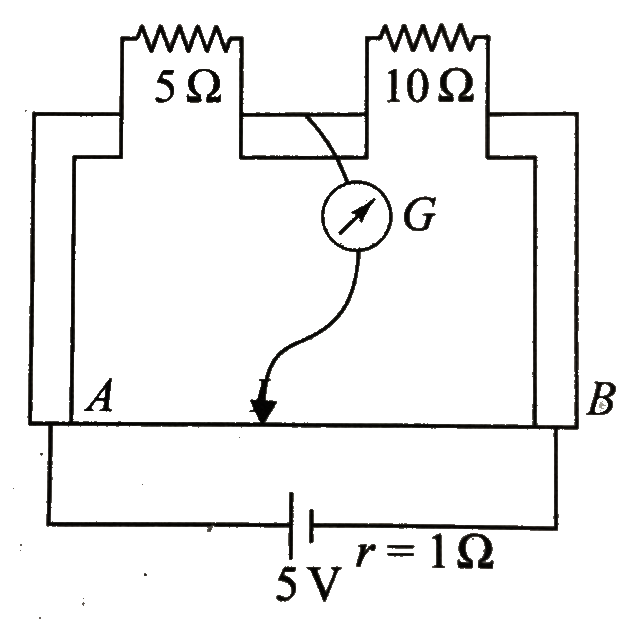 View Solution
View SolutionA wire of length 5m is twisted through 300 at free end If the radius of wire is 1mm , the shearing strain in the wire is
View SolutionA wire of length l has a resistance R. If half of the length is stretched to make the radius half of its original value, then the final resistance of the wire is
 View Solution
View SolutionCalculate the resistance of 1 km long copper wire of radius 1 mm. (Resistivity of copper is 1.72×10−8Ωm ).
View SolutionA wire of length 1m and radius 1mm is subjected to a load. The extension is x.The wire is melted and then drawn into a wire of square cross - section of side 2mm Its extension under the same load will be
View Solution

