the gauge pressure in both tyres of a bicycle is 690 k Pa. If the bicycle and the rider have a combined mass of 90 kg. what is the area of contact of each tyre with the ground? (assume that each tyre supports half the total weight of the bicycle.)
(a)6.39×10−4m2
(b)7.39×10−4m2
(c)8.39×10−4m2
(d)9.39×10−4m2
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Calculate the total weight of the bicycle and rider.
The total weight (W) can be calculated using the formula:
W=m⋅g
where:
- m=90kg (combined mass of the bicycle and rider)
- g=9.8m/s2 (acceleration due to gravity)
Calculation:
W=90kg⋅9.8m/s2=882N
Step 2: Determine the force supported by each tyre.
Since each tyre supports half of the total weight:
F=W2
Calculation:
F=882N2=441N
Step 3: Use the relationship between pressure, force, and area to find the area of contact.
The relationship is given by:
P=FA
where:
- P=690kPa=690×103Pa (convert kPa to Pa)
- F=441N
Rearranging the formula to find area (A):
A=FP
Calculation:
A=441N690×103Pa
Step 4: Perform the final calculation.
A=441690000≈6.39×10−4m2
Conclusion:
The area of contact of each tyre with the ground is approximately 6.39×10−4m2.
---
The total weight (W) can be calculated using the formula:
W=m⋅g
where:
- m=90kg (combined mass of the bicycle and rider)
- g=9.8m/s2 (acceleration due to gravity)
W=90kg⋅9.8m/s2=882N
Since each tyre supports half of the total weight:
F=W2
F=882N2=441N
The relationship is given by:
P=FA
where:
- P=690kPa=690×103Pa (convert kPa to Pa)
- F=441N
A=FP
A=441N690×103Pa
A=441690000≈6.39×10−4m2
The area of contact of each tyre with the ground is approximately 6.39×10−4m2.
Similar Questions
A track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2

View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View Solution
Knowledge Check
The mass of a bicycle rider along with the bicycle is 100 kg. he wants to cross over a circular turn of radius 100 m with a speed of 10ms−1. If the coefficient of friction between the tyres and the road is 0.6, will the rider be able to cross the turn? Take g=10ms−2.
A300NB600NC1200ND150N
Consider a vertical tube open at both ends. The tube consistss of two parts, each of different cross sections and each part having a piston which can move smoothly in respective tubes. The two piston which can move smoothly in respective tube wire. The piston are joined together by an inextensible wire. The combined mass of the two piston is 5kgand area of cross section of the upper piston is 10cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is 1mol. When the gas is heated slowly, pistons move by 50cm. Find the rise in the temperature of the gas in the form X/RK, where R is universal gas constant. Use g=10m/s2 and outside pressure =105N/m2).

View SolutionConsider a vertical tube open at both ends. The tube consistss of two parts, each of different cross sections and each part having a piston which can move smoothly in respective tubes. The two piston which can move smoothly in respective tube wire. The piston are joined together by an inextensible wire. The combined mass of the two piston is 5kgand area of cross section of the upper piston is 10cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is 1mol. When the gas is heated slowly, pistons move by 50cm. Find the rise in the temperature of the gas in the form X/RK, where R is universal gas constant. Use g=10m/s2 and outside pressure =105N/m2).

View SolutionA bicycle wheel of radius 0.3 m has a rim of mass 1.0 kg and 50 spokes, each of mass 0.01 kg. What is its moment of inertia about its axis of rotation ?
View SolutionA bicycle is traveling downhill at a high speed. Suddenly, the cyclist sees that a bridge ahead has collapsed, so she has to stop. What is the maximum magnitude of acceleration the bicycle can have if it is not to flip over its front wheel—in particular, if its rear wheel is not to leave the ground? The slope makes an angle of 37∘ with the horizontal. On level ground, the centre of mass of the woman–bicycle system is at a point 1.0m above the ground, 1.0m horizontally behind the axle of the front wheel, and 35.0 cm in front of the rear axle. Assume that the tires do not skid.
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
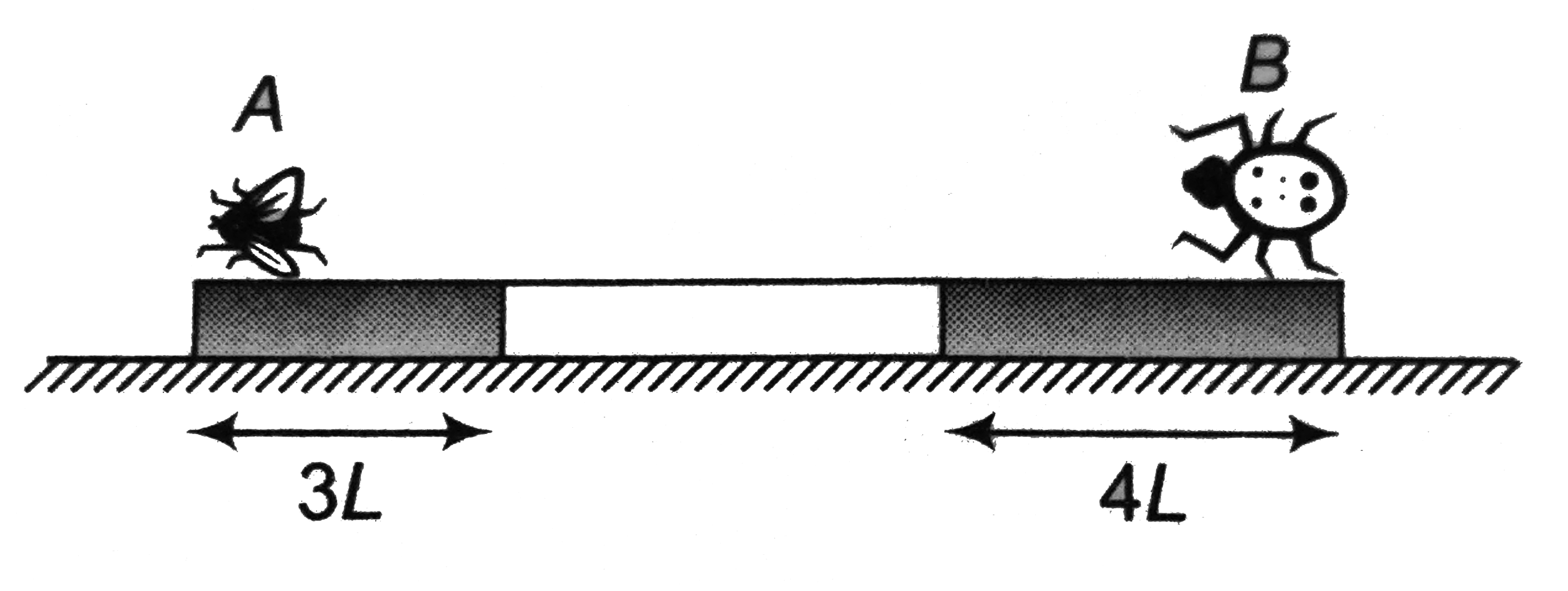
By what distance the centre of mass of the rod shifts during this time?
View SolutionA track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

View SolutionIn a tyre of "Ferrari" car of Mr. Obama, a tube having a volume of 12.3 litres is filled with air at a pressure of 4 atm at 300 K.Due to travelling, the temperature of the tube and air inside it raised to 360 K and pressure reduced to 3.6 atm in 20 minutes. If the porosity (number of pores per unit area) of the tube material is 5×103 pores/cm2 and each pore can transfer air from inside to outside of the tube with the rate of 6.023×108 molecules per minute.Calculate the total surface area (m2) of the tube.(R=0.082 Lt-atm/mole-K)
Give your answer divide by 100.
View Solution
