A 60 W , 120 V bulb is connected to a 240 V , 60 Hz supply with an inductance in series. Find the value of inductance so that bulb gets correct voltage.
2.3πH
2√3H
πH
2√3πH
The correct Answer is:D
To solve the problem of finding the inductance required for a 60 W, 120 V bulb connected to a 240 V, 60 Hz supply, we can follow these steps:
Step 1: Determine the resistance of the bulb
The power P of the bulb is given by the formula:
P=V2R
Where:
- P=60 W (power rating of the bulb)
- V=120 V (rated voltage of the bulb)
Rearranging the formula to find the resistance R:
R=V2P=120260=1440060=240Ω
Step 2: Calculate the current through the bulb
Using Ohm's Law, the current I through the bulb can be calculated as:
I=VR=120240=0.5A
Step 3: Calculate the total impedance Z
The total supply voltage Vs is 240 V. The impedance Z can be calculated using:
Z=VsI=2400.5=480Ω
Step 4: Relate impedance to resistance and inductive reactance
For an LR circuit, the impedance Z is given by:
Z=√R2+X2L
Where XL is the inductive reactance, given by XL=ωL and ω=2πf.
Step 5: Calculate ω
Given the frequency f=60 Hz:
ω=2πf=2π×60=120πrad/s
Step 6: Set up the equation for XL
From the impedance equation:
Z2=R2+X2L
Substituting the known values:
4802=2402+X2L
Calculating:
230400=57600+X2L
X2L=230400−57600=172800
XL=√172800=240√3Ω
Step 7: Calculate the inductance L
Using the relationship XL=ωL:
240√3=120πL
Rearranging for L:
L=240√3120π=2√3πH
Final Answer
The value of the inductance L required is:
L=2√3πH
The power P of the bulb is given by the formula:
P=V2R
Where:
- P=60 W (power rating of the bulb)
- V=120 V (rated voltage of the bulb)
R=V2P=120260=1440060=240Ω
Using Ohm's Law, the current I through the bulb can be calculated as:
I=VR=120240=0.5A
The total supply voltage Vs is 240 V. The impedance Z can be calculated using:
Z=VsI=2400.5=480Ω
For an LR circuit, the impedance Z is given by:
Z=√R2+X2L
Where XL is the inductive reactance, given by XL=ωL and ω=2πf.
Given the frequency f=60 Hz:
ω=2πf=2π×60=120πrad/s
From the impedance equation:
Z2=R2+X2L
Substituting the known values:
4802=2402+X2L
Calculating:
230400=57600+X2L
X2L=230400−57600=172800
XL=√172800=240√3Ω
Using the relationship XL=ωL:
240√3=120πL
Rearranging for L:
L=240√3120π=2√3πH
The value of the inductance L required is:
L=2√3πH
Similar Questions
An electric bulb is designed to consume 55W when operated at 110 volts. It is connected to a 220V,50Hz line through a choke coil in series. What should be the inductance of the coil for which the bulb gets correct voltage?
View SolutionA 100W200V bulb is connected to a 160V power supply. The power consumption would be
View SolutionTen 60 W, 220 V bulbs are connected in series to 220 V supply . Power consumed in the circuit is
View SolutionA 60μF capacitor is connected to a 110V, 60 Hz AC supply determine the rms value of the curent in the circuit.
View SolutionA coil of inductance 0.50H and resistance 100Ω is connected to a 240V, 50Hz ac supply. What are the maximum current in the coil and the time lag between voltage maximum and current maximum?
View SolutionOne 10V,60W bulb is to be connected to 100V line. The required inductance coil has self-inductance of value (f=50Hz)
View SolutionA 120 V, 60 W lamp is to be operated on 220 V, 50 Hz supply mains. Calculate what value of pure inductance which would be required so that the lamp runs on correct value of power.
View SolutionA 100W bulb is connected to an AC source of 220V, 50Hz. Then the current flowing through the bulb is
View SolutionThree 60W,120V light bulbs are connected across a 120V power lines as shown in Fig. 7.26. Find (a) the voltage across each bulb and (b) the total power dissipated in the three bulbs.
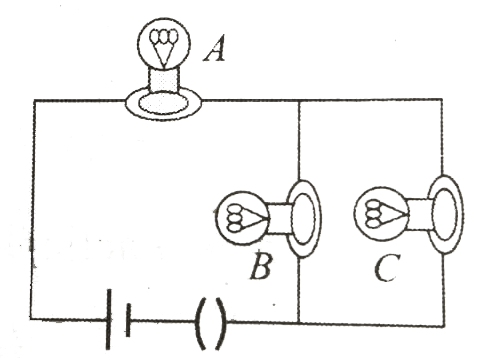
View SolutionThree 60 W, 120 V light bulbs are connected across a 120 V source as shown in figure. The total power dissipation in the three bulbs are
View Solution
