A battery of emf 12 V and internal resistance 2Ω is connected in series with a tangent galvanometer of resistance 4Ω . The deflection is 60∘ when the plane of the coil is along the magnetic meridian . To get a deflection of 30∘, the resistance to be connected in series with the tangent galvanometer is
12Ω
20Ω
10Ω
5Ω
The correct Answer is:A
To solve the problem, we need to determine the resistance that must be added in series with the tangent galvanometer to achieve a deflection of 30 degrees, given that the initial deflection is 60 degrees.
1. Identify the Given Values:
- EMF of the battery, E=12V
- Internal resistance of the battery, r=2Ω
- Resistance of the tangent galvanometer, Rg=4Ω
- Initial deflection angle, θ1=60∘
- Required deflection angle, θ2=30∘
2. Calculate the Initial Total Resistance:
The total resistance in the circuit when the galvanometer is connected is:
Rtotal=r+Rg=2Ω+4Ω=6Ω
3. Relate Current to Deflection:
The current through the galvanometer is proportional to the tangent of the angle of deflection:
I∝tan(θ)
Therefore, we can write:
I1I2=tan(θ1)tan(θ2)
4. Calculate the Tangents of the Angles:
- For θ1=60∘:
tan(60∘)=√3
- For θ2=30∘:
tan(30∘)=1√3
5. Set Up the Current Ratio:
Using the values of the tangents:
I1I2=√31√3=3
This means that the current I1 is three times the current I2.
6. Relate Currents to Resistances:
The current can also be expressed in terms of EMF and resistance:
I1=ERtotal=12V6Ω=2A
Therefore, for I2:
I2=I13=2A3=23A
7. Calculate the New Total Resistance for I2:
Using Ohm's law:
I2=ER′total⟹R′total=EI2=12V23A=18Ω
8. Determine the Additional Resistance Needed:
The new total resistance R′total includes the additional resistance R:
R′total=Rtotal+R⟹18Ω=6Ω+R
Solving for R:
R=18Ω−6Ω=12Ω
Final Answer:
The resistance to be connected in series with the tangent galvanometer is 12Ω.
- EMF of the battery, E=12V
- Internal resistance of the battery, r=2Ω
- Resistance of the tangent galvanometer, Rg=4Ω
- Initial deflection angle, θ1=60∘
- Required deflection angle, θ2=30∘
The total resistance in the circuit when the galvanometer is connected is:
Rtotal=r+Rg=2Ω+4Ω=6Ω
The current through the galvanometer is proportional to the tangent of the angle of deflection:
I∝tan(θ)
Therefore, we can write:
I1I2=tan(θ1)tan(θ2)
- For θ1=60∘:
tan(60∘)=√3
- For θ2=30∘:
tan(30∘)=1√3
Using the values of the tangents:
I1I2=√31√3=3
This means that the current I1 is three times the current I2.
The current can also be expressed in terms of EMF and resistance:
I1=ERtotal=12V6Ω=2A
Therefore, for I2:
I2=I13=2A3=23A
Using Ohm's law:
I2=ER′total⟹R′total=EI2=12V23A=18Ω
The new total resistance R′total includes the additional resistance R:
R′total=Rtotal+R⟹18Ω=6Ω+R
Solving for R:
R=18Ω−6Ω=12Ω
The resistance to be connected in series with the tangent galvanometer is 12Ω.
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View Solution
Knowledge Check
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A1100B1000C900D800A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7V
A cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
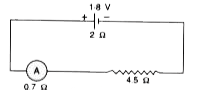
What would be the reading of the ammeter ?
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
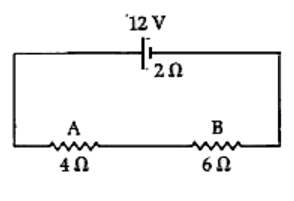
Find Electrical energy spent per minute in 4 Ω Resistor.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA galvanometer of resistance 50Ω given full-scale deflection for a current of 10 mA is to be changed into a voltmeter of rang 100 V . What should be the Value of resistance to be added in series with this galvanometer ?
View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View SolutionA galvanometer of resistance 1000Ω gives full-scale deflection for a current of 1mA. To measure a P.D of 10V, the resistance to be connected with the galvanometer is
View Solution
