Acceleration due to gravity at earth's surface is 10m−2 The value of acceleration due to gravity at the surface of a planet of mass 12 th and radius 12 of f the earth is -
5ms−2
10ms−2
20ms−2
40ms−2
The correct Answer is:C
To find the acceleration due to gravity at the surface of a planet with half the mass and half the radius of Earth, we can use the formula for gravitational acceleration:
g=G⋅MR2
where:
- g is the acceleration due to gravity,
- G is the universal gravitational constant,
- M is the mass of the planet,
- R is the radius of the planet.
1. Identify the given values:
- Acceleration due to gravity at Earth's surface, gE=10m/s2.
- Mass of the planet, M1=12ME (where ME is the mass of Earth).
- Radius of the planet, R1=12RE (where RE is the radius of Earth).
2. Write the formula for gravitational acceleration on the planet:
g1=G⋅M1R21
3. Substitute the values of M1 and R1:
g1=G⋅(12ME)(12RE)2
4. Simplify the denominator:
(12RE)2=14R2E
Thus, we can rewrite g1:
g1=G⋅(12ME)14R2E
5. Simplify the expression:
g1=G⋅MER2E⋅1/21/4=G⋅MER2E⋅2
Therefore:
g1=2⋅G⋅MER2E
6. Substitute the value of gE:
Since G⋅MER2E=gE=10m/s2:
g1=2⋅10m/s2=20m/s2
7. Conclusion:
The acceleration due to gravity at the surface of the planet is:
g1=20m/s2
Final Answer:
The value of acceleration due to gravity at the surface of the planet is 20 m/s².
- g is the acceleration due to gravity,
- G is the universal gravitational constant,
- M is the mass of the planet,
- R is the radius of the planet.
- Acceleration due to gravity at Earth's surface, gE=10m/s2.
- Mass of the planet, M1=12ME (where ME is the mass of Earth).
- Radius of the planet, R1=12RE (where RE is the radius of Earth).
g1=G⋅M1R21
g1=G⋅(12ME)(12RE)2
(12RE)2=14R2E
Thus, we can rewrite g1:
g1=G⋅(12ME)14R2E
g1=G⋅MER2E⋅1/21/4=G⋅MER2E⋅2
Therefore:
g1=2⋅G⋅MER2E
Since G⋅MER2E=gE=10m/s2:
g1=2⋅10m/s2=20m/s2
The acceleration due to gravity at the surface of the planet is:
g1=20m/s2
The value of acceleration due to gravity at the surface of the planet is 20 m/s².
Similar Questions
The value of acceleration due to gravity at the surface of earth
View SolutionHow is the acceleration due to gravity on the surface of the earth related to its mass and radius ?
View SolutionThe ratio of acceleration due to gravity at a height 3 R above earth's surface to the acceleration due to gravity on the surface of earth is
(R = radius of earth)
View SolutionAcceleration due to gravity is ‘ g ’ on the surface of the earth. The value of acceleration due to gravity at a height of 32 km above earth’s surface is (Radius of the earth = 6400 km )
View SolutionThe acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionAcceleration due to gravity at earth's surface if 'g' m/s2. Find the effective value of acceleration due to gravity at a height of 32 km from sea level : (Re=6400km)
View SolutionIf accleration due to gravity on the surface of earth is 10ms−2 and let acceleration due to gravitational acceleration at surface of another planet of our solar system be 5ms−2 An astronaut weighing 50kg on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by
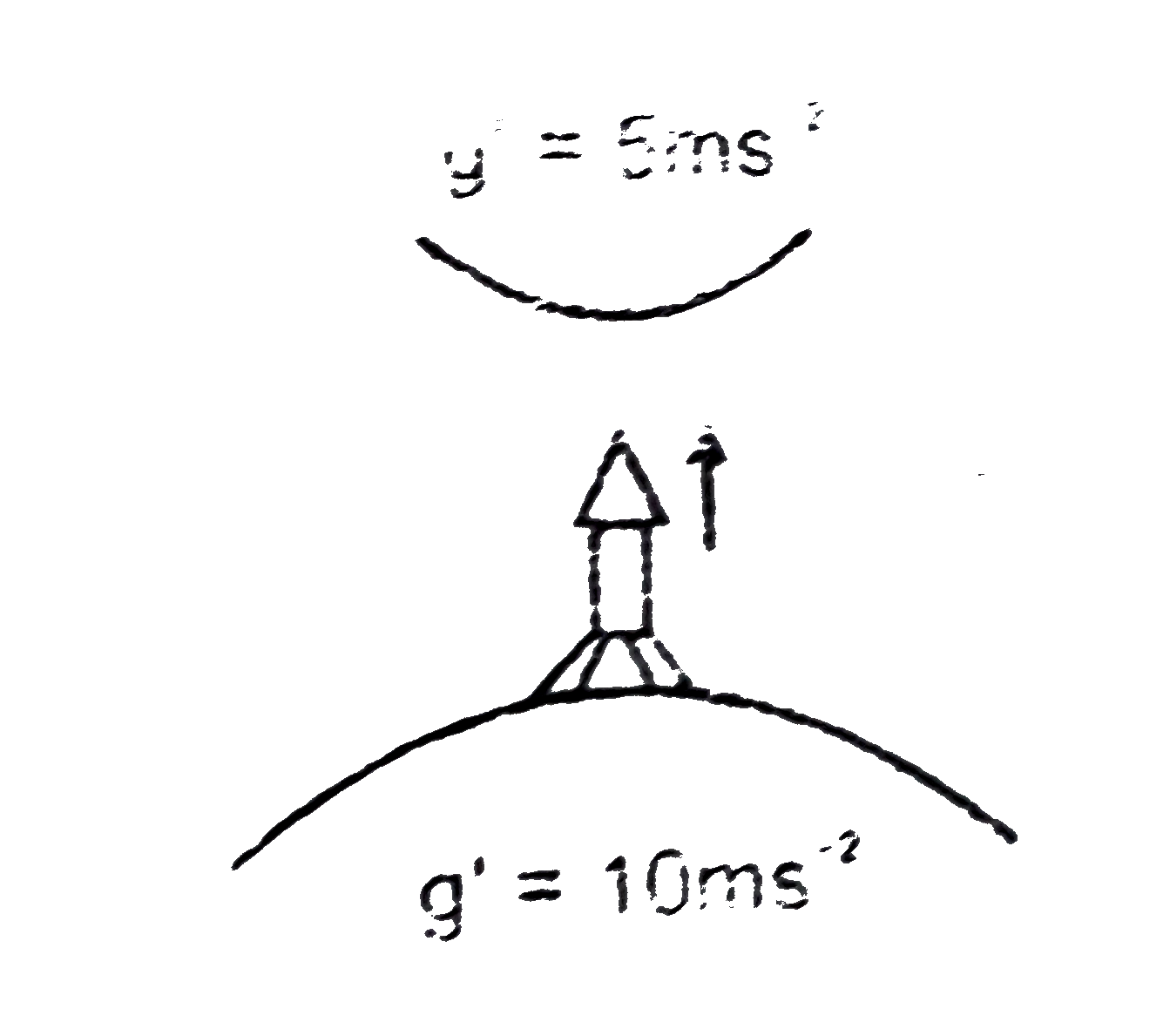 .
.
View SolutionIf g1 and g2 denote acceleration due to gravity on the surface of the earth and on a planet whose mass and radius is thrice that of earth, then
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View Solution
