In an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
12Ω
8Ω
16Ω
1Ω
The correct Answer is:B
To find the internal resistance of the cell using the given data from the potentiometer experiment, we can follow these steps:
Step 1: Understand the Setup
In the experiment, we have a cell with an internal resistance r and an electromotive force (EMF) E. The cell is shunted by two different resistances: R1=4Ω and R2=8Ω. The balance points on the potentiometer wire are L1=2m for R1 and L2=3m for R2.
Step 2: Write the Equations for Each Case
For the first case (shunted by 4Ω):
Er+R1=V0L1
Substituting R1=4Ω and L1=2m:
Er+4=V02(1)
For the second case (shunted by 8Ω):
Er+R2=V0L2
Substituting R2=8Ω and L2=3m:
Er+8=V03(2)
Step 3: Eliminate E and V0
From equations (1) and (2), we can eliminate E and V0 by dividing the two equations:
Er+4÷Er+8=V0/2V0/3
This simplifies to:
r+8r+4=32
Step 4: Cross Multiply and Solve for r
Cross multiplying gives:
2(r+8)=3(r+4)
Expanding both sides:
2r+16=3r+12
Rearranging gives:
16−12=3r−2r
4=r
Step 5: Conclusion
Thus, the internal resistance of the cell is:
4Ω
In the experiment, we have a cell with an internal resistance r and an electromotive force (EMF) E. The cell is shunted by two different resistances: R1=4Ω and R2=8Ω. The balance points on the potentiometer wire are L1=2m for R1 and L2=3m for R2.
For the first case (shunted by 4Ω):
Er+R1=V0L1
Substituting R1=4Ω and L1=2m:
Er+4=V02(1)
Er+R2=V0L2
Substituting R2=8Ω and L2=3m:
Er+8=V03(2)
From equations (1) and (2), we can eliminate E and V0 by dividing the two equations:
Er+4÷Er+8=V0/2V0/3
This simplifies to:
r+8r+4=32
Cross multiplying gives:
2(r+8)=3(r+4)
Expanding both sides:
2r+16=3r+12
Rearranging gives:
16−12=3r−2r
4=r
Thus, the internal resistance of the cell is:
4Ω
Similar Questions
In an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionInternal resistance of a cell depends on
View Solution
Knowledge Check
In a potentiometer the balancing with a cell is at length of 220cm. On shunting the cell with a resistance of 3Ω balance length becomes 130cm. What is the internal resistance of this cell.
A4.5ΩB7.8ΩC6.3ΩD2.08Ω
In an experiment on the measurement of internal resistance of as cell by using a potentionmeter, when the key K is kept open then balancing length is obtained at y metre. When the key K is closed and some resistance R is inserted in the resistance box, then the balancing length is found to be x metre. Then the internal resistance is
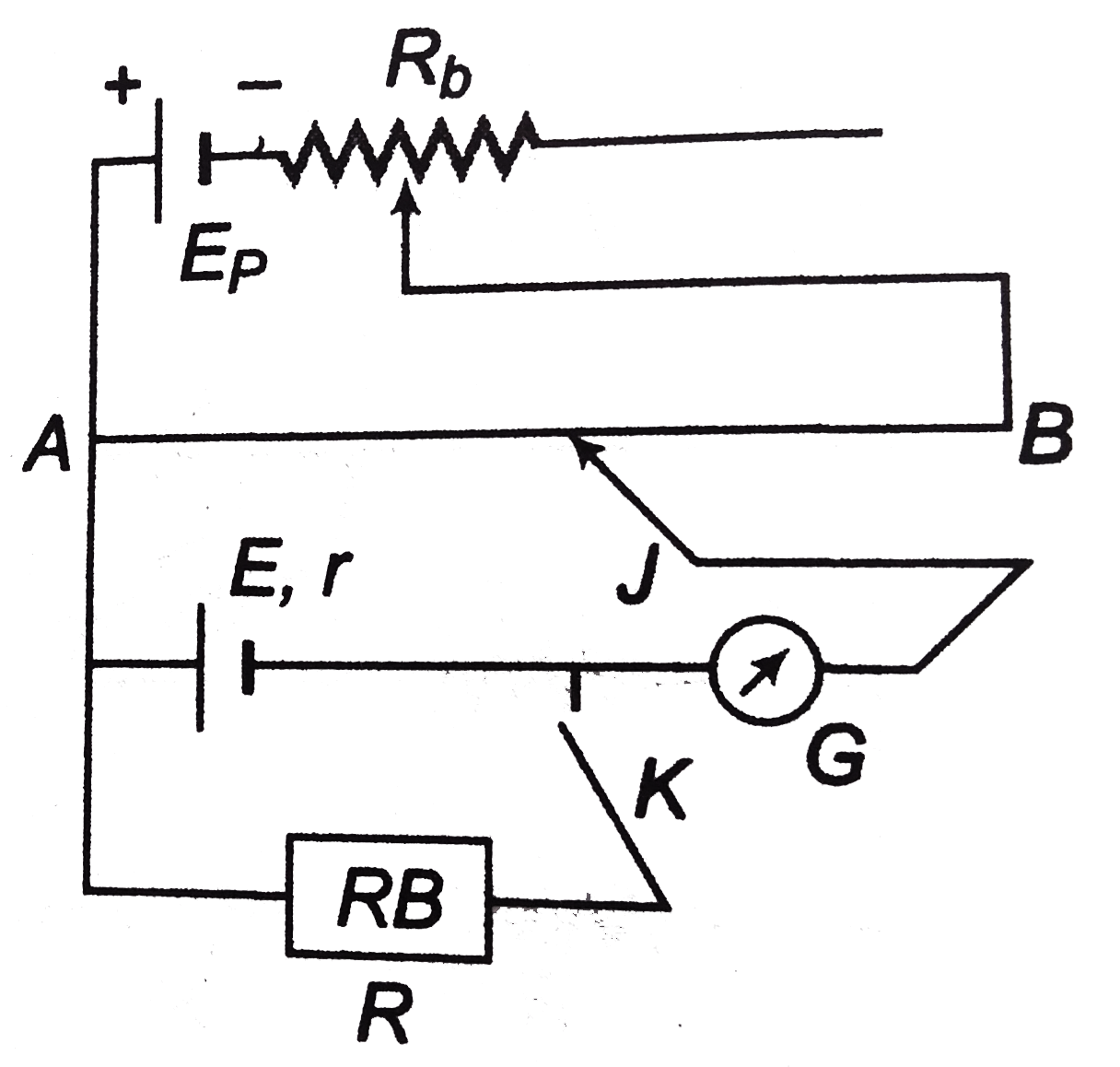
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionFor a cell of e.m.f. 2 V , a balance is obtained for 50 cm of the potentiometer wire. If the cell is shunted by a 2Ω resistor and the balance is obtained across 40 cm of the wire, then the internal resistance of the cell is
View SolutionA Daniel cell is balanced on 125cm length of a potentiometer wire. Now the cells is short-circuited by a resistance 2ohm and the balance is obtained at 100cm. The internal resistance of the Dainel cell is
View SolutionA battery is connected to a potentiometer and a balance point is obtained at 84cm along the wire. When its terminals are connected by a 5Ω resistor, the balance point changes to 70cm.
Calculate the internal resistance of the cell.
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionThe terminal voltage is E2 when a c urrent of 2A is flowing through 2Ω resistance, then the internal resistance of cell is:-
View Solution
