A body of mass 1g and carrying a charge 10−8C passes from two points P and Q. P and Q are at electric potentials 600 V and 0 V respectively. The velocity of the body at Q is 20 cms−1. It velocity in ms−1at P is
√0.028
√0.056
√0.56
√5.6
The correct Answer is:A
To solve the problem step by step, we will use the principle of conservation of energy. The total mechanical energy (kinetic energy + potential energy) remains constant when a charged body moves in an electric field.
Step 1: Understand the Given Data
- Mass of the body, m=1g=1×10−3kg
- Charge of the body, q=10−8C
- Electric potential at point P, VP=600V
- Electric potential at point Q, VQ=0V
- Velocity at point Q, V2=20cm/s=20×10−2m/s=0.2m/s
Step 2: Write the Energy Conservation Equation
The conservation of energy states that the gain in kinetic energy is equal to the loss in potential energy. Therefore, we can write:
Gain in K.E.=Loss in P.E.
This can be expressed mathematically as:
12mV21−12mV22=qVP−qVQ
Step 3: Substitute Known Values
Substituting the known values into the equation:
12(1×10−3)V21−12(1×10−3)(0.2)2=(10−8)(600)−(10−8)(0)
Step 4: Simplify the Equation
This simplifies to:
12(1×10−3)V21−12(1×10−3)(0.04)=6×10−6
Now, simplifying further:
12(1×10−3)V21−2×10−5=6×10−6
Step 5: Rearranging the Equation
Rearranging gives:
12(1×10−3)V21=6×10−6+2×10−5
Calculating the right side:
6×10−6+2×10−5=2.6×10−5
So we have:
12(1×10−3)V21=2.6×10−5
Step 6: Solve for V21
Multiplying both sides by 2:
(1×10−3)V21=5.2×10−5
Now, divide by 1×10−3:
V21=5.2×10−51×10−3=5.2×10−2
Step 7: Take the Square Root
Taking the square root gives:
V1=√5.2×10−2≈0.228m/s
Final Answer
The velocity of the body at point P is approximately 0.228m/s.
---
- Mass of the body, m=1g=1×10−3kg
- Charge of the body, q=10−8C
- Electric potential at point P, VP=600V
- Electric potential at point Q, VQ=0V
- Velocity at point Q, V2=20cm/s=20×10−2m/s=0.2m/s
The conservation of energy states that the gain in kinetic energy is equal to the loss in potential energy. Therefore, we can write:
Substituting the known values into the equation:
This simplifies to:
Rearranging gives:
Multiplying both sides by 2:
Taking the square root gives:
The velocity of the body at point P is approximately 0.228m/s.
Similar Questions
Two points P and Q are maintained at the potentials of 10V and -4V, respectively. The work done in moving 100 electrons from P to Q is:
View SolutionA ball of mass 1g and charge 10−8C moves from a point A. Where potential is 600 volt to the point B where potential is zero. Velocity of the ball at the point B is 20cm/s. The velocity of the ball at the point A will be
View SolutionA mass of 1kg carrying a charge of 2C is accelerated through a potential of 1V. The velocity acquired by it is
View SolutionLet C1 and C2 be parabolas x2=y−1 and y2=x−1 respectively. Let P be any point on C1 and Q be any point C2. Let P1 and Q1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P1 lies on C2 and Q1 lies on C1 and PQ≥[PP1,QQ1]. Hence or otherwise , determine points P0 and Q0 on the parabolas C1 and C2 respectively such that P0Q0≤PQ for all pairs of points (P,Q) with P on C1 and Q on C2
View SolutionIf in the circuit shown below, the internal resistance of the battery is 1.5Ω and VP and VQ are the potential at P and Q respectively, what is the potential difference between the point P and Q?
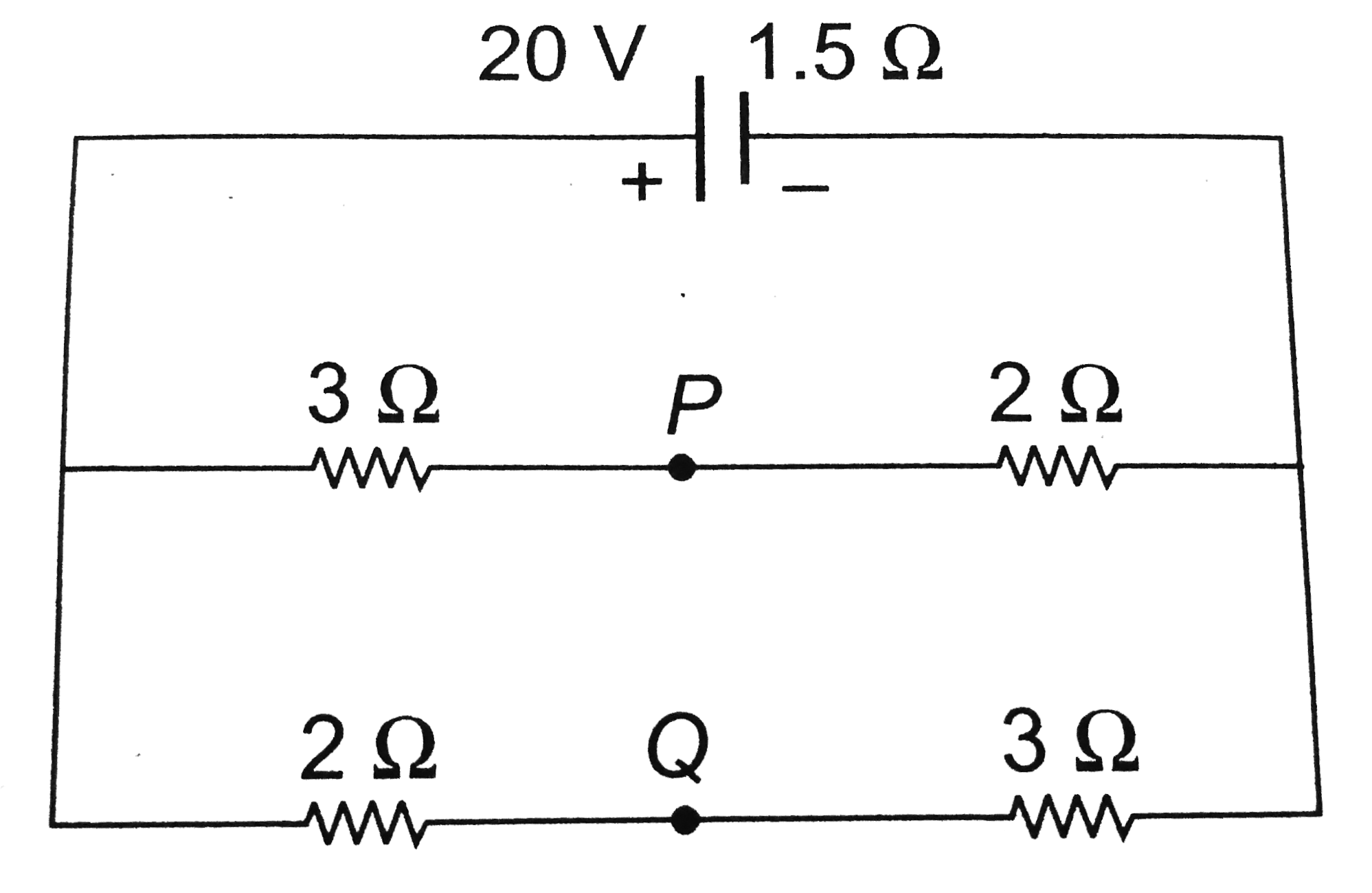
View SolutionIf v2,v2, and v3 are the velocities of points P,C and Q respectively lying on body doing pure rolling motion, then correct order of velocities will be
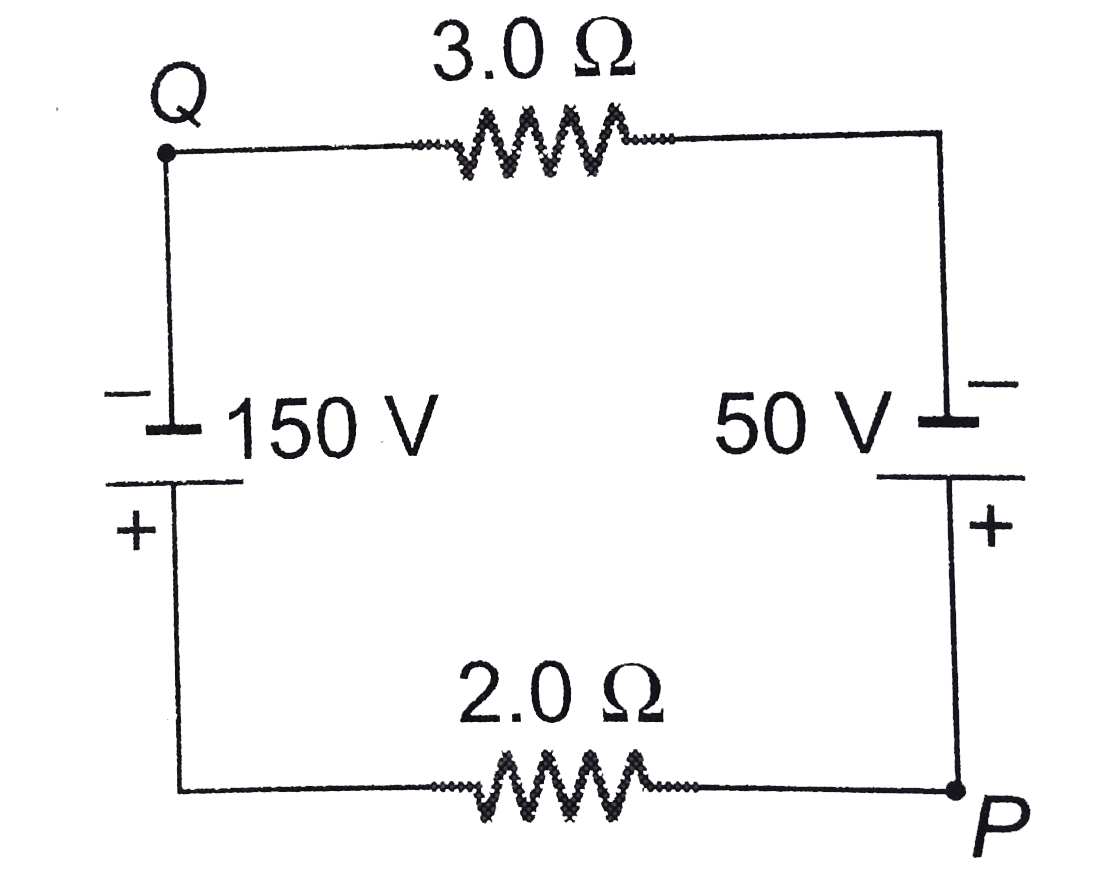
View SolutionIn Figure if the potential at Point P is 100V, what is the potential at point Q?
View SolutionLet C1 and C2 be respectively, the parabolas x2=y−1 and y2=x−1 Let P be any point on C1 and Q be any point on C2 . Let P1 and Q1 be the refelections of P and Q, respectively with respect to the line y=x.
If the point p(π,π2+1) and Q(μ2+1,μ) then P1 and Q1 are
View SolutionA spherical shell of radius 10 cm is carrying a charge q. If the electric potential at distances 5 cm, 10 cm and 15 cm from the centre of the spherical shell is V1,V2 and V3 respectively, then
View SolutionTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
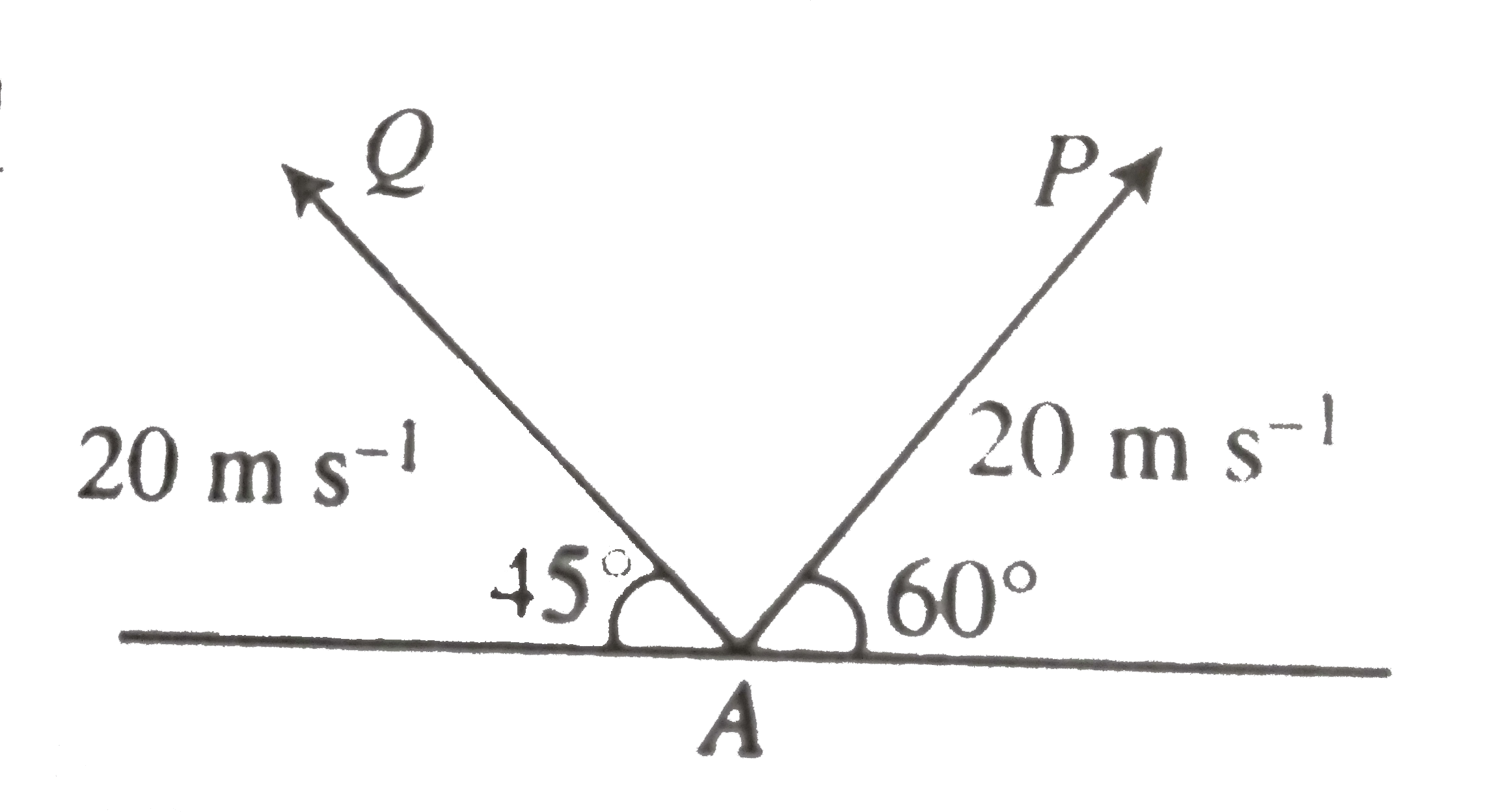
View Solution
