A metal ball hits a wall and does not rebound whereas a rubber ball of the same mass on hitting the wall the same velocity rebounds back. It can be concluded that–
metal ball suffers greater change in momentum
rubber ball suffers greater change in momentum .
the initial momentum of metal ball is greater than the initial momentum of rubber ball.
both suffer same change in momentum .
The correct Answer is:B
To solve the problem, we need to analyze the collision of the two balls (metal and rubber) with the wall in terms of momentum change.
1. Understanding the Scenario:
- A metal ball hits a wall and does not rebound.
- A rubber ball of the same mass hits the wall and rebounds back.
- Both balls are initially moving towards the wall with the same velocity.
2. Defining Momentum:
- Momentum (p) is defined as the product of mass (m) and velocity (v):
p=mv
3. Calculating Initial Momentum:
- For both balls before hitting the wall, the initial momentum is:
pinitial=mv(for both balls)
4. Calculating Final Momentum:
- For the metal ball:
- After hitting the wall, it does not rebound, so its final velocity is 0.
- Therefore, the final momentum of the metal ball is:
pfinal, metal=0
- For the rubber ball:
- After hitting the wall, it rebounds back with the same speed but in the opposite direction.
- If we consider the direction towards the wall as positive, the final momentum of the rubber ball is:
pfinal, rubber=−mv
5. Calculating Change in Momentum:
- Change in momentum is calculated as:
Δp=pfinal−pinitial
- For the metal ball:
Δpmetal=0−mv=−mv
- For the rubber ball:
Δprubber=−mv−mv=−2mv
6. Comparing Changes in Momentum:
- The change in momentum for the metal ball is −mv.
- The change in momentum for the rubber ball is −2mv.
- This indicates that the rubber ball experiences a greater change in momentum compared to the metal ball.
7. Conclusion:
- From the analysis, we can conclude that the rubber ball suffers a greater change in momentum than the metal ball.
Final Answer:
The rubber ball suffers a greater change in momentum than the metal ball.
- A metal ball hits a wall and does not rebound.
- A rubber ball of the same mass hits the wall and rebounds back.
- Both balls are initially moving towards the wall with the same velocity.
- Momentum (p) is defined as the product of mass (m) and velocity (v):
p=mv
- For both balls before hitting the wall, the initial momentum is:
pinitial=mv(for both balls)
- For the metal ball:
- After hitting the wall, it does not rebound, so its final velocity is 0.
- Therefore, the final momentum of the metal ball is:
pfinal, metal=0
- For the rubber ball:
- After hitting the wall, it rebounds back with the same speed but in the opposite direction.
- If we consider the direction towards the wall as positive, the final momentum of the rubber ball is:
pfinal, rubber=−mv
- Change in momentum is calculated as:
Δp=pfinal−pinitial
- For the metal ball:
Δpmetal=0−mv=−mv
- For the rubber ball:
Δprubber=−mv−mv=−2mv
- The change in momentum for the metal ball is −mv.
- The change in momentum for the rubber ball is −2mv.
- This indicates that the rubber ball experiences a greater change in momentum compared to the metal ball.
- From the analysis, we can conclude that the rubber ball suffers a greater change in momentum than the metal ball.
The rubber ball suffers a greater change in momentum than the metal ball.
Similar Questions
A metalic ball strikes a wall and drops dead whereas tennis ball having the same mass and velocity bounces back. Which of the following is correct ?
View SolutionA rubber ball falls from a height h and rebounds to a height h/2. A rubber ball of double the mass falling from the same height h rebounds to a height
View Solution
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzero
A ball hits a floor and rebounds after an inelastic collision. In this case
View SolutionA ball moves on a smooth floor in a straight line with a uniform velocity 10 m s−1 for 6 s. At t = 6 s, the ball hits a wall and comes back along the same line to the starting point with same speed. Draw the velocity-time graph and use it to find the total distance travelled by the ball and its displacement.
View SolutionA surface is hit elastically and normally by n bals per unit time, all the balls having the same mass m, and moving with the same velocity v. then the force acting on surface is
View SolutionA small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n/2. All surfaces are smooth. Find the value of n.

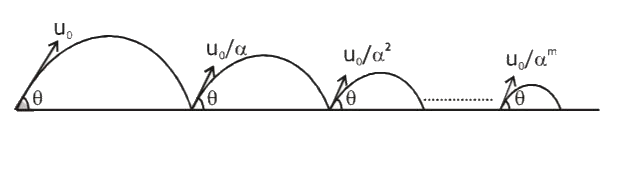
View SolutionA ball is thrown from ground at an angle θ with horizontal and with an initial speed u0 . For the resulting projectile motion, the magnitude of average velocity of the ball up to the point when it hits the ground for the first time is V1 . After hitting the ground, the ball rebounds at the same angle θ but with a reduced speed of u0 / α . Its motion continues for a long time as shown in figure. If the magnitude of average velocity of the ball for entire duration of motion is 0.8 V1 ,. the value of α is ________.
View SolutionFind the impulse experienced by a body.If the body mass M hits normally a rigid wall with velocity v and bounces back with the same speed.
View SolutionA boy throws a ball with a velocity u at an angle θ with the horizontal. At the same instant he starts running with uniform velocity to catch the ball before it hits the ground. To achieve this he should run with a velocity of
View Solution
