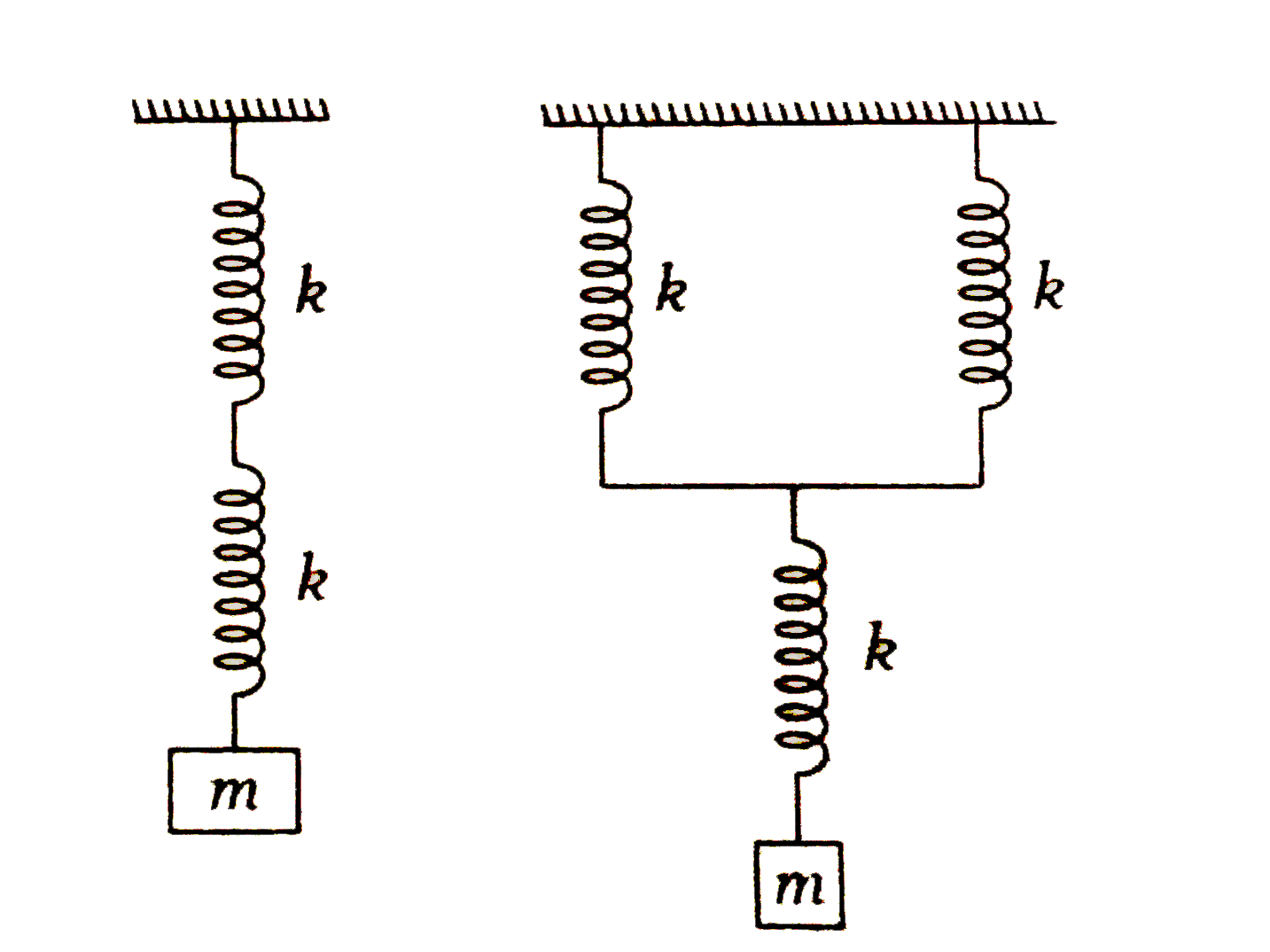
Two identical springs are connected in parallel and series as shown in the figure. If fpandfs are frequencies of arrangements , what is fsfp ?
1:2
2:1
1:3
3:1
The correct Answer is:A
To solve the problem of finding the ratio of frequencies fsfp for two identical springs connected in series and parallel, we can follow these steps:
Step 1: Understand the frequency formula
The frequency f of a spring system is given by the formula:
f=12π√KM
where K is the spring constant and M is the mass attached to the spring.
Step 2: Identify the spring constants for series and parallel arrangements
1. For springs in series:
The equivalent spring constant Ks for two identical springs (each with spring constant K) connected in series is given by:
1Ks=1K+1K=2K⟹Ks=K2
2. For springs in parallel:
The equivalent spring constant Kp for two identical springs connected in parallel is given by:
Kp=K+K=2K
Step 3: Write the frequencies for both arrangements
1. Frequency for springs in series:
fs=12π√KsM=12π√K/2M=12π√K2M
2. Frequency for springs in parallel:
fp=12π√KpM=12π√2KM
Step 4: Find the ratio of the frequencies
Now, we can find the ratio fsfp:
fsfp=12π√K2M12π√2KM=√K2M√2KM
Step 5: Simplify the ratio
Simplifying the above expression:
fsfp=√K√2M⋅√M√2K=√K⋅√M√2M⋅√2K=1√4=12
Thus, the ratio fsfp is:
fsfp=12
Final Answer
The ratio fsfp is 12.
The frequency f of a spring system is given by the formula:
f=12π√KM
where K is the spring constant and M is the mass attached to the spring.
1. For springs in series:
The equivalent spring constant Ks for two identical springs (each with spring constant K) connected in series is given by:
1Ks=1K+1K=2K⟹Ks=K2
The equivalent spring constant Kp for two identical springs connected in parallel is given by:
Kp=K+K=2K
1. Frequency for springs in series:
fs=12π√KsM=12π√K/2M=12π√K2M
fp=12π√KpM=12π√2KM
Now, we can find the ratio fsfp:
fsfp=12π√K2M12π√2KM=√K2M√2KM
Simplifying the above expression:
fsfp=√K√2M⋅√M√2K=√K⋅√M√2M⋅√2K=1√4=12
fsfp=12
The ratio fsfp is 12.
Similar Questions
Two identical spring of constant K are connected in series and parallel as shown in figure. A mass is suspended from them. The ratio of their frequencies of vertical oscillations will be
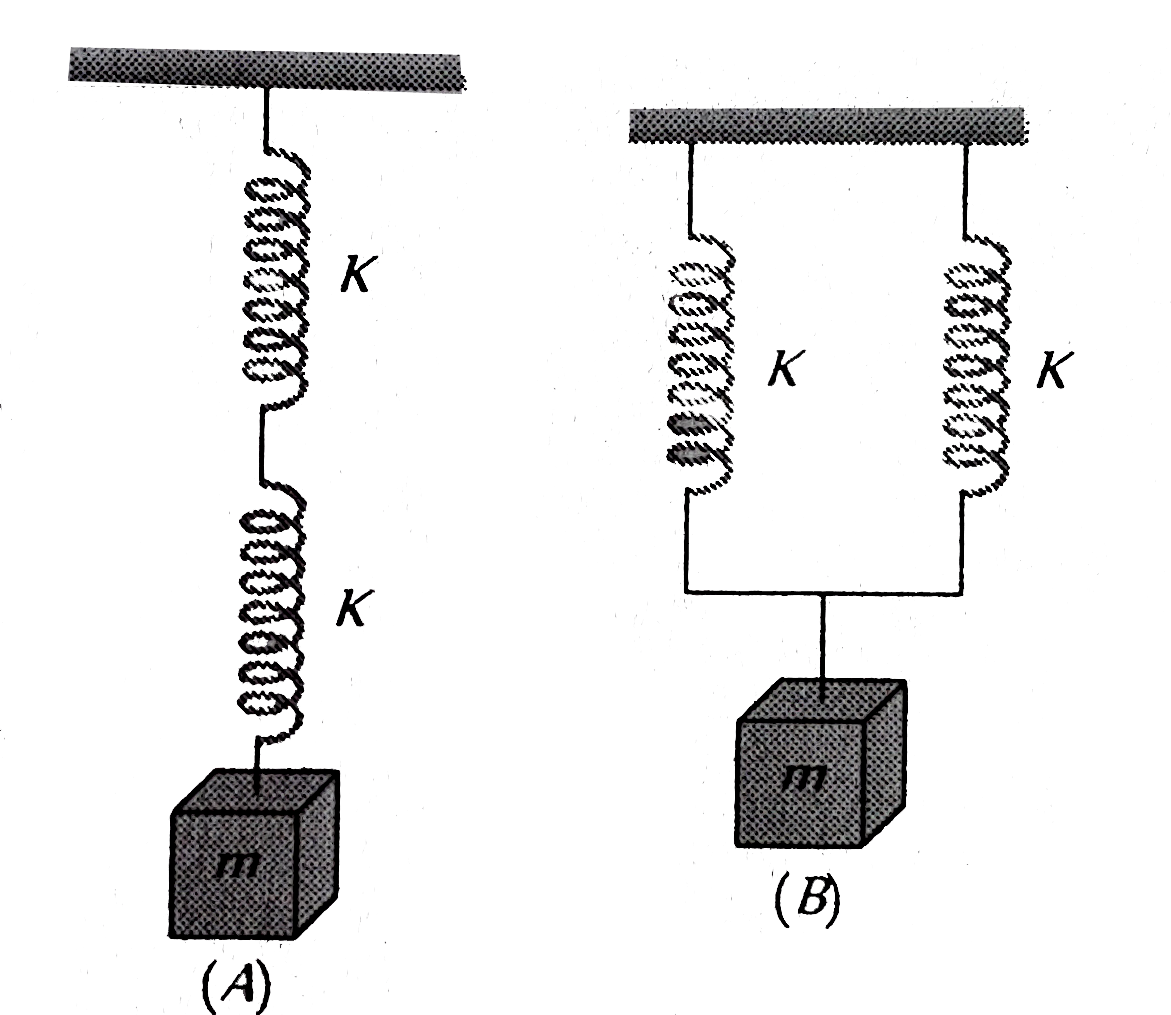
View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
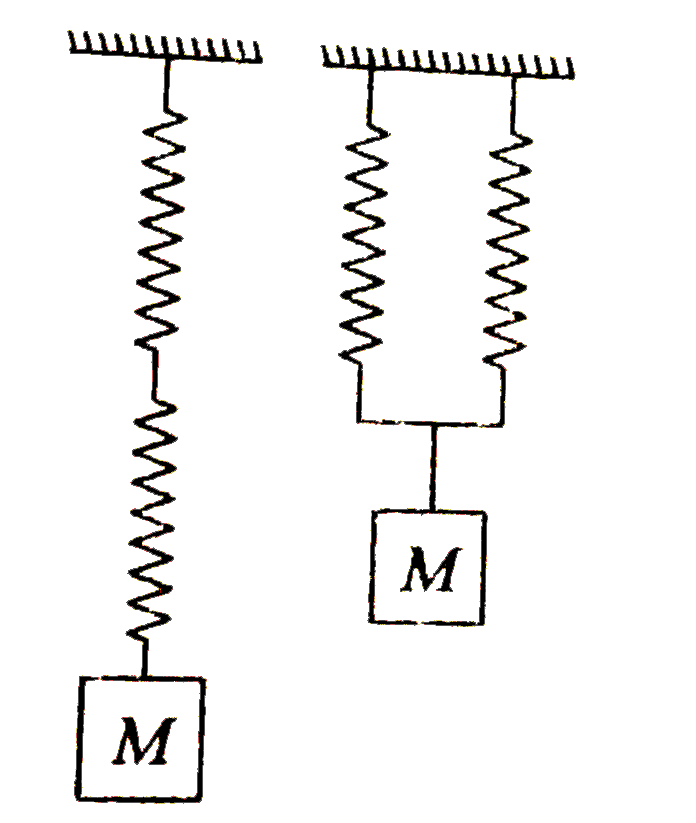
View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View SolutionSome springs are combined in series and parallel arrangement as shown in the figure and a mass m is suspended from them. The ratio of their frequencies will be
View SolutionTwo identical incandescent light bulbs are connected as shown in figure. When the circuit is an AC voltage source of frequency f, which of the following observations will be correct.
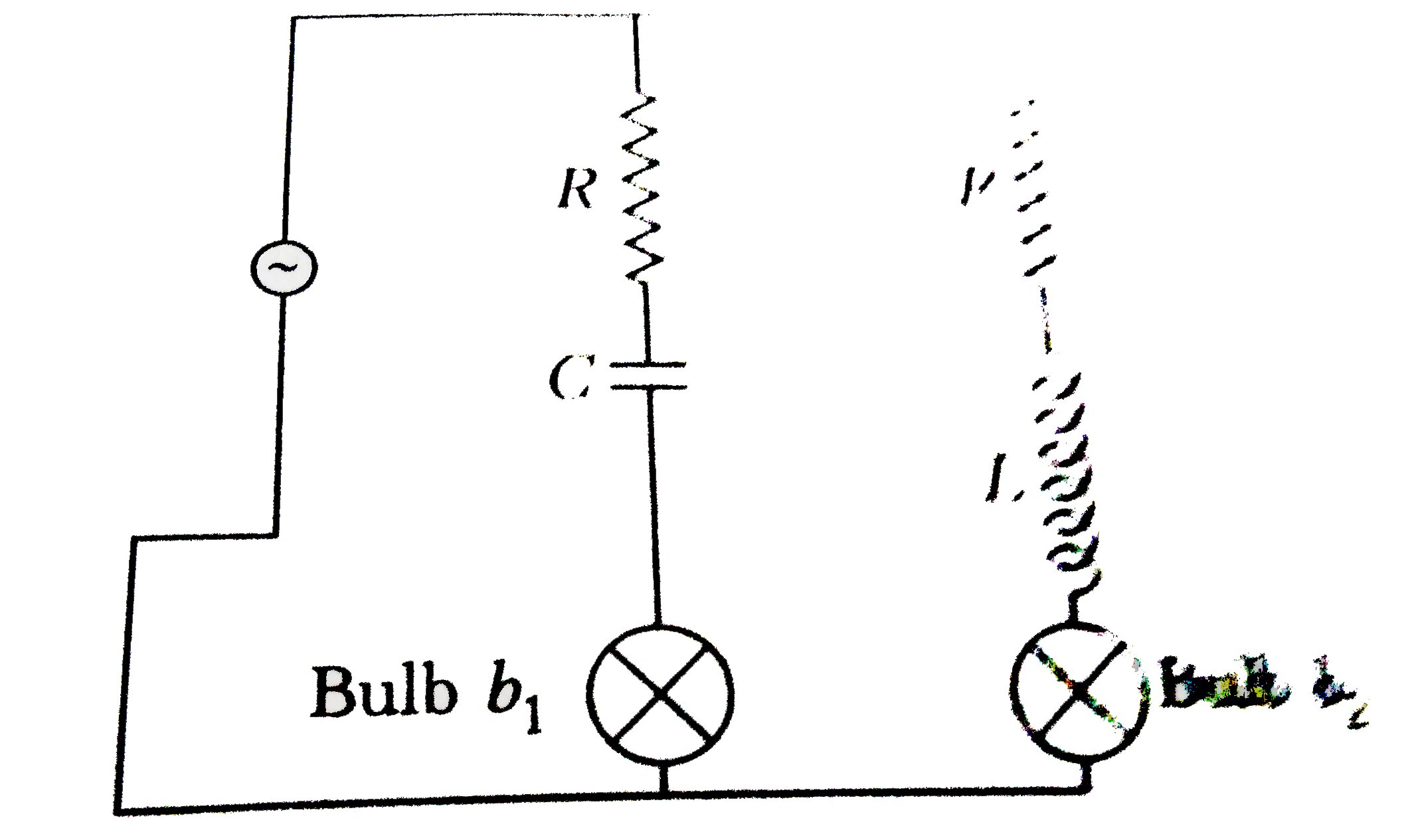
View SolutionTwo identical tubes A and B are kept in air and water respetively as shown. If the fundamental frequency of A is f0, then thr fundamental frequency of B is
View SolutionConsider the arrangement shown in figure. Friction coefficient for all the surfaces are shown in the figure and the rod connecting two upper blocks is horizontal.
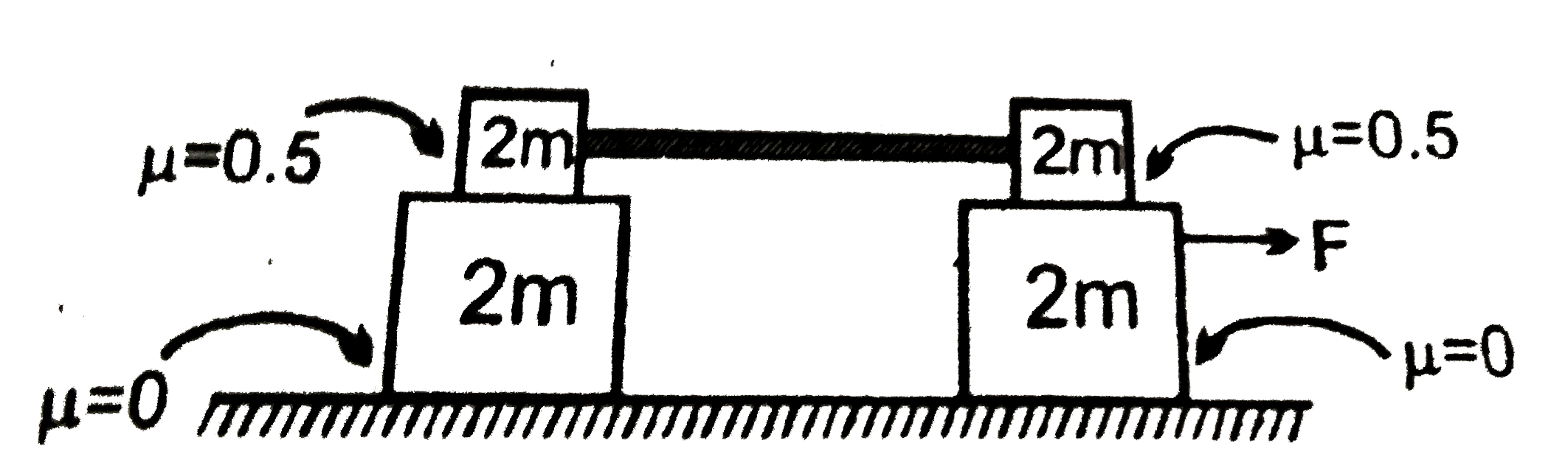
What is the minimum value F so that the rear two blocks start sliding with each other :
View SolutionFor the arrangement as shown in the figure the maximum force F, for no relative motion between blocks is

View SolutionFour open organ popes of different length and different gases at same temperature as shown in figure. Let fA,fB,fC and fD be their fundamental frequencies then : [Take γCO2=43]
_E01_065_Q01.png) .
.
View Solution
