The ratio of radii of nuclei .13A127 and .52XA is 3:5. The number of neutrons in the nuclei of X will be
52
73
125
13
The correct Answer is:B
To solve the problem, we need to find the number of neutrons in the nucleus of element X given the ratio of the radii of the nuclei of aluminum and X.
1. Understanding the Relationship Between Radius and Mass Number:
The radius r of a nucleus is related to its mass number A by the formula:
r∝A1/3
This means that the radius of a nucleus is proportional to the cube root of its mass number.
2. Setting Up the Ratio of Radii:
Given the ratio of the radii of the nuclei of aluminum (Al) and element X:
rAlrX=35
We can express this in terms of their mass numbers AAl and AX:
rAlrX=(AAlAX)1/3
3. Substituting Known Values:
The mass number of aluminum is given as AAl=27. Thus, we can write:
35=(27AX)1/3
4. Cubing Both Sides:
To eliminate the cube root, we cube both sides:
(35)3=27AX
This simplifies to:
27125=27AX
5. Solving for AX:
By cross-multiplying, we find:
27⋅AX=27⋅125
Dividing both sides by 27 gives:
AX=125
6. Finding the Number of Neutrons:
The number of neutrons N in the nucleus can be calculated using the formula:
N=A−Z
where Z is the atomic number (number of protons). For element X, Z=52:
N=125−52=73
Final Answer:
The number of neutrons in the nucleus of element X is 73.
---
The radius r of a nucleus is related to its mass number A by the formula:
r∝A1/3
This means that the radius of a nucleus is proportional to the cube root of its mass number.
Given the ratio of the radii of the nuclei of aluminum (Al) and element X:
rAlrX=35
We can express this in terms of their mass numbers AAl and AX:
rAlrX=(AAlAX)1/3
The mass number of aluminum is given as AAl=27. Thus, we can write:
35=(27AX)1/3
To eliminate the cube root, we cube both sides:
(35)3=27AX
This simplifies to:
27125=27AX
By cross-multiplying, we find:
27⋅AX=27⋅125
Dividing both sides by 27 gives:
AX=125
The number of neutrons N in the nucleus can be calculated using the formula:
N=A−Z
where Z is the atomic number (number of protons). For element X, Z=52:
N=125−52=73
The number of neutrons in the nucleus of element X is 73.
Similar Questions
The ratio of the radii of the nuclei .2713Al and .52Te125 is approximately-
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
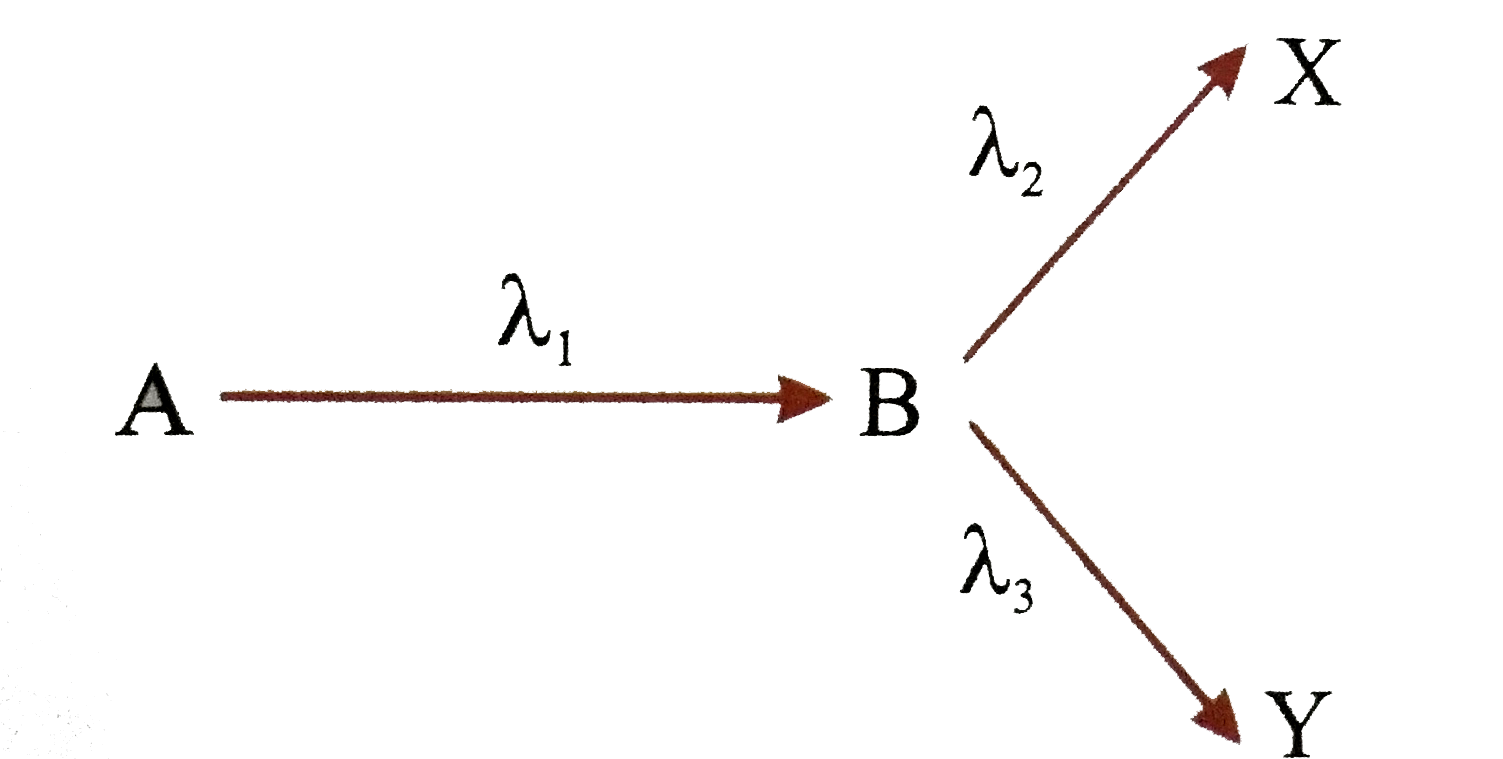
The number of nuclei of B will first increase and then after a maximum value, it decreases for
View SolutionA radio nuclide X is produced at constant rate α. At time t=0, number of nuclei of X are zero. Find
(a) the maximum number of nuclei of X.
the number of nuclei at time t.
Decay constant of X is λ.
View SolutionStatement : The plot of atomic number ( y -axis ) versus number of neutrons ( x -axis ) for stable nuclei shows a curvature towards x-axis fron the line of 45∘ slope as the atomic number is increased .
Explanation : proton -proton electrostatic repulsions begin to overcome attracive forces involving protons and neutrons in heavier nuclides.
View SolutionAssuming the radius of a nucleus to be equal to R=1.3A1/3×10−15m. Where A is its mass number, evaluate the density of nuclei and the number of nucleons per unit volume of the nucleus. Take mass of one nucleon =1.67×10−27kg
View SolutionThe rate of biomass production by consumers is called :
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio (n/p). For stable nuclei n/p ratio lies close to unity for elements with low atmoic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having n/p ratio either very high or low undergo nuclear transformation. When n/p ratio is higher than required for stability, the nuclei have the tendency to emit β-rays. while when n/p ratio is lower than required for stability, the nuclei either emits α-particles or a positron or capture K-electron.
For reaction .92M238→.yNx+2.2He4,.yNx→.BLA+2.−1e0
The number of neutrons in the element L is
View SolutionTwo radioactive materials X1 and X2 have decay constants 10λ and λ respectively. If initially they have the same number of nuclei, if the ratio of the number of nuclei of X1 to that of X2 will be 1/e after a time n9λ. Find the value of n?
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionTwo radioactive X1 and X2 have decay constants 10λ and λ respectively . If initially they have the same number of nuclei, then the ratio of the number of nuclei of X1 to that of X2will be 1/e after a time .
View Solution
