A circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
λ3√3ε0R
2λ3√3ε0R2
23√3λε0R
none the these
The correct Answer is:A
To find the electric field at the point (0,0,R√2) due to a circular ring of radius R with uniform linear charge density λ, we can follow these steps:
Step 1: Understand the Geometry
The circular ring lies in the x-y plane, centered at the origin. The point where we want to calculate the electric field is located on the z-axis at a distance R√2 above the center of the ring.
Step 2: Use the Formula for Electric Field on the Axis of a Ring
The electric field E at a point along the axis of a charged ring can be calculated using the formula:
E=k⋅Q⋅z(z2+R2)3/2
where:
- k=14πϵ0 is Coulomb's constant,
- Q is the total charge on the ring,
- z is the distance from the center of the ring to the point along the axis,
- R is the radius of the ring.
Step 3: Calculate the Total Charge Q
The total charge Q on the ring can be calculated as:
Q=λ⋅L
where L is the circumference of the ring, given by L=2πR. Thus,
Q=λ⋅2πR
Step 4: Substitute Values into the Electric Field Formula
Substituting Q into the electric field formula, we have:
E=k⋅(λ⋅2πR)⋅(R√2)((R√2)2+R2)3/2
Step 5: Simplify the Denominator
Calculating (R√2)2+R2:
(R√2)2=R22
Thus,
R22+R2=R22+2R22=3R22
Now, substituting this back into the electric field equation:
E=k⋅(λ⋅2πR)⋅(R√2)(3R22)3/2
Step 6: Calculate the Denominator
Calculating (3R22)3/2:
(3R22)3/2=(33/2R323/2)=3√3R32√2
Step 7: Substitute Back and Simplify
Now substituting this back into the electric field expression:
E=k⋅(λ⋅2πR)⋅(R√2)3√3R32√2
This simplifies to:
E=2kλπR23√3R32√2⋅1√2
Step 8: Final Simplification
After simplification, we find:
E=4kλπ√23√3R
Step 9: Substitute k
Substituting k=14πϵ0:
E=4⋅14πϵ0⋅λ⋅π√23√3R
This results in:
E=λ√23√3ϵ0R
Final Answer
Thus, the electric field at the point (0,0,R√2) is:
E=λ√23√3ϵ0R
The circular ring lies in the x-y plane, centered at the origin. The point where we want to calculate the electric field is located on the z-axis at a distance R√2 above the center of the ring.
The electric field E at a point along the axis of a charged ring can be calculated using the formula:
- k=14πϵ0 is Coulomb's constant,
- Q is the total charge on the ring,
- z is the distance from the center of the ring to the point along the axis,
- R is the radius of the ring.
The total charge Q on the ring can be calculated as:
Substituting Q into the electric field formula, we have:
Calculating (R√2)2+R2:
Calculating (3R22)3/2:
Now substituting this back into the electric field expression:
After simplification, we find:
Substituting k=14πϵ0:
Thus, the electric field at the point (0,0,R√2) is:
Similar Questions
A circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View Solution
Knowledge Check
A magnetic field B is confined to a region r≤ a and points out of the paper (the z-axis), r = 0 being the center of the circular region. A charged ring (charge = Q) of radius b and mass m lie in the x-y plane with its center at origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time Δt. Find the angular velocity ω of the ring after the field vanishes.
AqBa22mbBqBa2mb2C2b2qBa2Dqb22Ba2
A circular ring carries a uniformly distributed positive charge and lies in the xy plane with center at the origin of the cooredinate system. If at a point (0,0,z) the electric field is E, then which of the following graphs is correct?
View SolutionA solid non conducting sphere of radius R and uniform volume charge density ρ has its centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R/2,0,0) (ii) (R√2,R√2,0) (iii) (R,R,0)
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density σc/m3. It has a spherical cavity of radius R as shown in the figure. The electric field at the centre of the cavity is
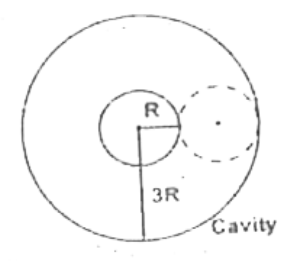
View SolutionA circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View SolutionA magnetic field B is confined to a region r≤ a and points out of the paper (the z-axis), r = 0 being the centre of the cicular region. A charged ring (charge = Q) of radius b,bgt a and mass m lie in the x-y plane with its centre at origin. The ring is free to rotate and is at rest. The magnetic field is brougth to zero in time Δt. Find the angular velocity omega or the ring after the field vanishes.
View SolutionA positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
View Solution
