A circular coil of radius 4 cm having 50 turns carries a current of 2 A . It is placed in a uniform magnetic field of the intensity of 0.1 Weber m−2 . The work done to rotate the coil from the position by 180∘ from the equilibrium position
0.1 J
0.2 J
0.4 J
0.8 J
The correct Answer is:A
To solve the problem, we need to calculate the work done in rotating a circular coil in a magnetic field. Here are the steps to arrive at the solution:
Step 1: Calculate the Area of the Coil
The area A of a circular coil is given by the formula:
A=πr2
where r is the radius of the coil. Given that the radius r=4 cm, we first convert it to meters:
r=4cm=0.04m
Now, substituting the value of r:
A=π(0.04)2=π(0.0016)=0.0016πm2
Step 2: Calculate the Magnetic Moment
The magnetic moment μ of the coil is given by:
μ=n⋅I⋅A
where n is the number of turns, I is the current, and A is the area calculated in Step 1. Given n=50 turns and I=2 A:
μ=50⋅2⋅(0.0016π)=100⋅0.0016π=0.16πA m2
Step 3: Calculate the Work Done
The work done W in rotating the coil in a magnetic field is given by the change in potential energy:
W=μB(cosθi−cosθf)
where:
- B is the magnetic field intensity (given as 0.1Wb/m2),
- θi is the initial angle (0 degrees),
- θf is the final angle (180 degrees).
Substituting the values:
cosθi=cos(0)=1
cosθf=cos(180)=−1
Thus,
W=μB(1−(−1))=μB(1+1)=2μB
Step 4: Substitute the Values
Now substituting μ=0.16π and B=0.1:
W=2⋅(0.16π)⋅(0.1)=0.032πJ
Step 5: Calculate the Numerical Value
Using π≈3.14:
W≈0.032⋅3.14≈0.10048J
Final Answer
The work done to rotate the coil by 180∘ from the equilibrium position is approximately:
W≈0.1J
The area A of a circular coil is given by the formula:
A=πr2
where r is the radius of the coil. Given that the radius r=4 cm, we first convert it to meters:
r=4cm=0.04m
Now, substituting the value of r:
A=π(0.04)2=π(0.0016)=0.0016πm2
The magnetic moment μ of the coil is given by:
μ=n⋅I⋅A
where n is the number of turns, I is the current, and A is the area calculated in Step 1. Given n=50 turns and I=2 A:
μ=50⋅2⋅(0.0016π)=100⋅0.0016π=0.16πA m2
The work done W in rotating the coil in a magnetic field is given by the change in potential energy:
W=μB(cosθi−cosθf)
where:
- B is the magnetic field intensity (given as 0.1Wb/m2),
- θi is the initial angle (0 degrees),
- θf is the final angle (180 degrees).
cosθi=cos(0)=1
cosθf=cos(180)=−1
Thus,
W=μB(1−(−1))=μB(1+1)=2μB
Now substituting μ=0.16π and B=0.1:
W=2⋅(0.16π)⋅(0.1)=0.032πJ
Using π≈3.14:
W≈0.032⋅3.14≈0.10048J
The work done to rotate the coil by 180∘ from the equilibrium position is approximately:
W≈0.1J
Similar Questions
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
A circular coil of radius 4 cm has 50 turns. In this coil a current of 2 A is flowing. It is placed in a magnetic field of 0.1weber/m2. The amount of work done in rotating it through 180∘ from its equilibrium position will be
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
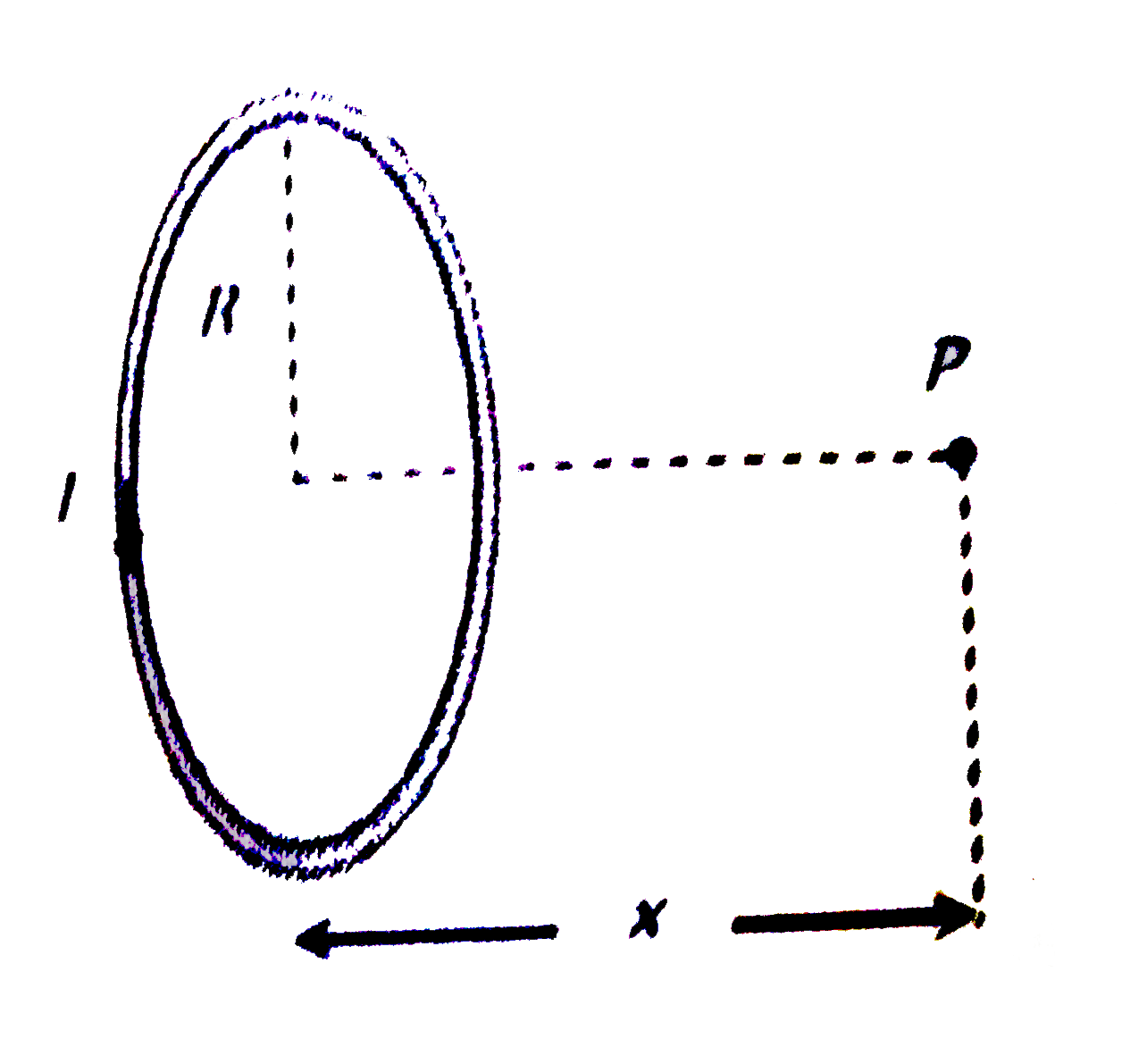
View SolutionA rectangular loop of area 5m2, has 50 turns and carries a current of 1A. It is held in a uniform magnetic field of 0.1T, at an angle of 30∘. Calculate the torque experienced by the coil.
View SolutionA circular coil having 50 turns, each with an area of 0.01 m, carries a current of 2 A. Calculate its magnetic dipole moment.
View SolutionA 100 turn closely wound circular coil of radius 10cm carries a current of 3⋅2A.What is the field at the centre of the coil?
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View Solution
