A charge particle is moving in a uniform magnetic field ib a circular path. The energy of the particle is doubled . If the initial radius of he circular path was R, the radius of the new circular path after the energy is doubled will be
R2
√2R
2R
R√2
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the energy of a charged particle moving in a magnetic field and the radius of its circular path.
1. Understanding the Motion of the Charged Particle:
A charged particle moving in a uniform magnetic field describes a circular path due to the Lorentz force acting as the centripetal force. The magnetic force acting on the particle is given by:
F=qvB
where q is the charge, v is the velocity, and B is the magnetic field strength.
2. Centripetal Force:
The centripetal force required to keep the particle in circular motion is given by:
F=mv2r
where m is the mass of the particle and r is the radius of the circular path.
3. Equating Forces:
Setting the magnetic force equal to the centripetal force, we have:
qvB=mv2r
4. Solving for Velocity:
Rearranging the equation to solve for v:
v=qBrm
5. Kinetic Energy of the Particle:
The kinetic energy E of the particle is given by:
E=12mv2
Substituting v from the previous step:
E=12m(qBrm)2=12q2B2r2m
6. Energy Proportionality:
From the expression for energy, we can see that the energy E is directly proportional to r2:
E∝r2
7. Doubling the Energy:
If the energy is doubled, we can express this as:
E2=2E1
Therefore, we have:
2E1∝r22
8. Setting Up the Ratio:
Since E1∝r21, we can write:
E2E1=r22r21
Substituting E2=2E1:
2=r22r21
9. Finding the New Radius:
Rearranging gives:
r22=2r21
Taking the square root:
r2=r1√2
10. Final Result:
If the initial radius r1=R, then the new radius r2 is:
r2=R√2
Conclusion:
The radius of the new circular path after the energy is doubled will be R√2.
---
A charged particle moving in a uniform magnetic field describes a circular path due to the Lorentz force acting as the centripetal force. The magnetic force acting on the particle is given by:
F=qvB
where q is the charge, v is the velocity, and B is the magnetic field strength.
The centripetal force required to keep the particle in circular motion is given by:
F=mv2r
where m is the mass of the particle and r is the radius of the circular path.
Setting the magnetic force equal to the centripetal force, we have:
qvB=mv2r
Rearranging the equation to solve for v:
v=qBrm
The kinetic energy E of the particle is given by:
E=12mv2
Substituting v from the previous step:
E=12m(qBrm)2=12q2B2r2m
From the expression for energy, we can see that the energy E is directly proportional to r2:
E∝r2
If the energy is doubled, we can express this as:
E2=2E1
Therefore, we have:
2E1∝r22
Since E1∝r21, we can write:
E2E1=r22r21
Substituting E2=2E1:
2=r22r21
Rearranging gives:
r22=2r21
Taking the square root:
r2=r1√2
If the initial radius r1=R, then the new radius r2 is:
r2=R√2
The radius of the new circular path after the energy is doubled will be R√2.
Similar Questions
Knowledge Check
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which :
Aits speed remains constant.Bits velocity remains constant.Cits momentum remains constant.Dits kinetic energy increases.A charged particle is moving on circular path with velocityv in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes
A8 timesB4 timesC2 timesD16 timesA particle revolves round a circular path with uniform speed. The acceleration of the particle is
Aalong the circumference of the circle.Balong the tangentCalong the radiusDzero
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which:
View SolutionA charged particle moves in a circular path in a uniform magnetic field. If its speed is reduced, then its tiem period will
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
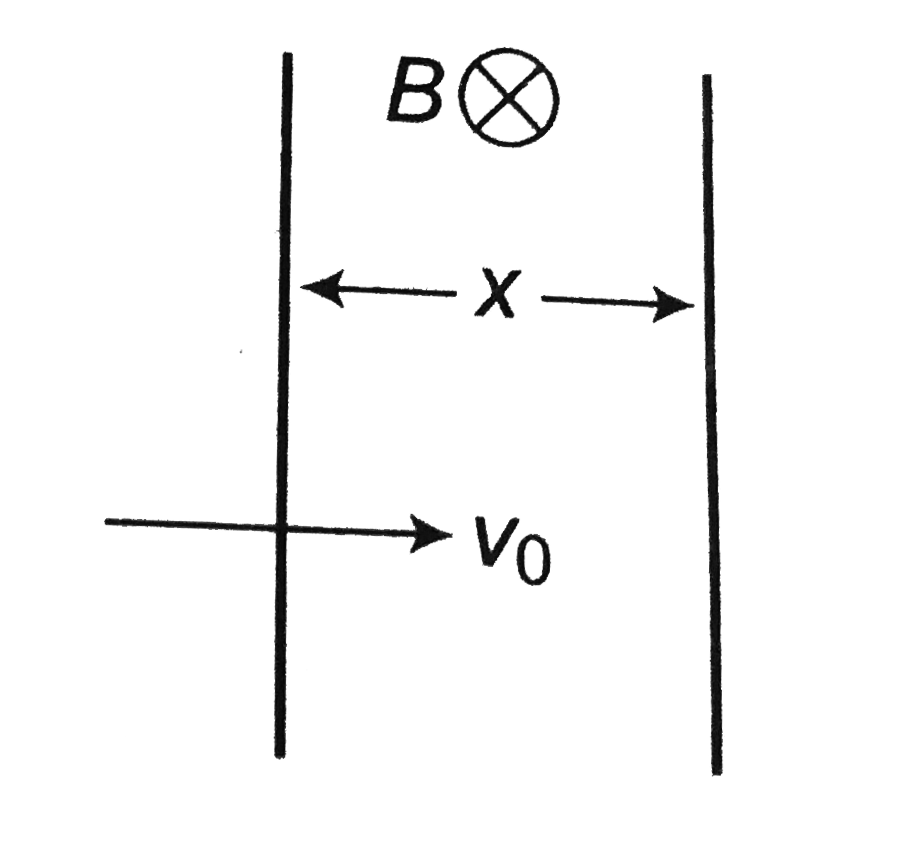
View Solution

