A body is projected vertically upwatds at time t=0 and is it seen at a height H at time t1 and t2 second during its flight. The maximum height attainet is (g is acceleration due to garavity).
g4(t1+t2)2
g(t1+t24)2
2g(t1+t24)2
g4(t1t2)
The correct Answer is:C
To find the maximum height attained by a body projected vertically upwards, given that it is seen at a height H at times t1 and t2, we can follow these steps:
Step 1: Understand the motion of the body
When a body is projected upwards, it will rise to a maximum height and then fall back down. The times t1 and t2 indicate two instances when the body is at the same height H during its ascent and descent.
Step 2: Relate the times t1 and t2
The time taken to go from height H to the maximum height is equal to the time taken to fall from the maximum height back down to height H. Therefore, the average time taken to reach the maximum height after reaching H can be expressed as:
tavg=t1+t22
Step 3: Determine the total time of flight
The total time of flight T can be expressed as:
T=t2+(t2−t1)=t1+t2
Step 4: Use the kinematic equation for height
The height H at time t can be expressed using the kinematic equation:
H=ut−12gt2
where u is the initial velocity and g is the acceleration due to gravity.
Step 5: Substitute the average time into the height equation
Substituting t=t1+t22 into the height equation gives:
H=u(t1+t22)−12g(t1+t22)2
Step 6: Rearranging for maximum height
The maximum height Hmax can be derived from the time of flight. The time to reach maximum height tmax is equal to T2=t1+t22. The maximum height can be expressed as:
Hmax=u⋅tmax−12gt2max
Step 7: Substitute tmax
Substituting tmax=t1+t22:
Hmax=u⋅t1+t22−12g(t1+t22)2
Step 8: Simplify the expression
This can be simplified to:
Hmax=(t1+t2)u2−g(t1+t2)28
Step 9: Find the relationship between H and Hmax
From the earlier equations, we can derive:
H=g8(t1+t2)2
Thus, the maximum height attained can be expressed as:
Hmax=g8(t1+t2)2
Conclusion
The maximum height attained by the body is:
Hmax=g8(t1+t2)2
When a body is projected upwards, it will rise to a maximum height and then fall back down. The times t1 and t2 indicate two instances when the body is at the same height H during its ascent and descent.
The time taken to go from height H to the maximum height is equal to the time taken to fall from the maximum height back down to height H. Therefore, the average time taken to reach the maximum height after reaching H can be expressed as:
tavg=t1+t22
The total time of flight T can be expressed as:
T=t2+(t2−t1)=t1+t2
The height H at time t can be expressed using the kinematic equation:
H=ut−12gt2
where u is the initial velocity and g is the acceleration due to gravity.
Substituting t=t1+t22 into the height equation gives:
H=u(t1+t22)−12g(t1+t22)2
The maximum height Hmax can be derived from the time of flight. The time to reach maximum height tmax is equal to T2=t1+t22. The maximum height can be expressed as:
Hmax=u⋅tmax−12gt2max
Substituting tmax=t1+t22:
Hmax=u⋅t1+t22−12g(t1+t22)2
This can be simplified to:
Hmax=(t1+t2)u2−g(t1+t2)28
From the earlier equations, we can derive:
H=g8(t1+t2)2
Thus, the maximum height attained can be expressed as:
Hmax=g8(t1+t2)2
The maximum height attained by the body is:
Hmax=g8(t1+t2)2
Similar Questions
A rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
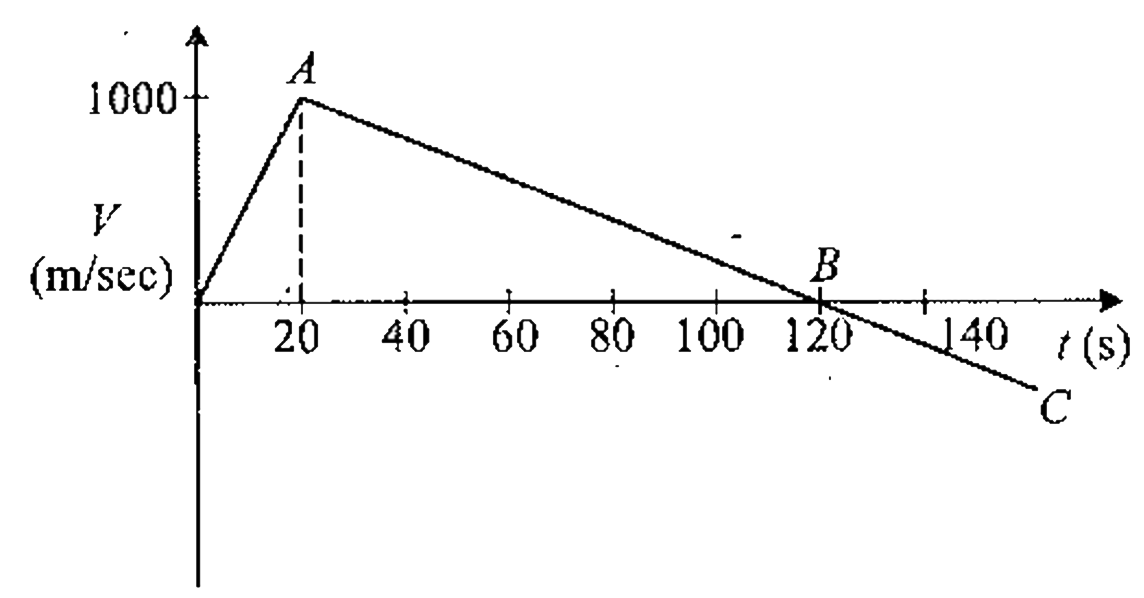
View SolutionA body is projected vertically upwards with speed √gRe from the surface of earth. What is the maximum height attained by the body ? [Re is the radius of earth, g is acceleration due to gravity]
View Solution
Knowledge Check
A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
Ag(t−T)2BH−12g(t−T)2C12g(t−T)2DH−g(t−T)2
A body is projected up with velocity u. It reaches a point in its path at times t1 and t2 seconds from the time of projection. Then (t1+t2) is
View SolutionA ball is projected vertically up such that it passes thorugh a fixed point after a time t1 and t2 respectively. Find
a. The height at which the point is located with respect to the point of projeciton
b. The speed of projection of the ball.
c. The velocity the ball at the time of passing through point P.
d. (i) The maximum height reached by the balll relative to the point of projection A (ii) maximum height reached by the ball relative to point P under consideration.
e. The average speed and average velocity of the ball during the motion from A to P for the time t1 and t2 respectively.
 .
.
View SolutionA particle is projected vertically upwards and reaches the maximum height H in time T. The height of the partlcle at any time t(<T) will be
View SolutionA ball is projected vertically upward with speed of 50 m/s. Find a. the maximum height, b. the time to reach the maximum height, c. the speed at half the maximum height. Take g=10ms2.
View SolutionA body is projected at an angle θ so that its range is maximum. If T is the time of flight then the value of maximum range is (acceleration due to gravity= g)
View SolutionA ball is projected vertically upward with a speed of 50m/s. Find (a) the maximum height, (b) the time to reach the maximum height, (c) the speed at half the maximum height. Take g=10ms2.
View SolutionA body is projected up with a speed u and the time taken by it is T to reach the maximum height H. Pich out the correct statement
View Solution
