An electric dipole is fixed at the origin of coordinates. Its moment is directed in the positive x- direction. A positive charge is moved from the point (r,0) to the point (−r,0) by an external agent. In this process, the work done by the agent is
positive and inversely proportional to r
positive and inversely proportional to r2
negative and inversely proportional to r
negative and inversely proportional to r2
The correct Answer is:D
To solve the problem of finding the work done by an external agent when moving a positive charge from point (r, 0) to point (-r, 0) in the presence of a fixed electric dipole, we can follow these steps:
Step 1: Understand the Configuration
We have an electric dipole fixed at the origin with its dipole moment →P directed along the positive x-direction. A positive charge is moved from point A(r,0) to point B(−r,0).
Step 2: Calculate the Electric Potential Energy at Points A and B
The electric potential V due to a dipole at a point →r is given by:
V=k→P⋅^rr2
where k is a constant, →P is the dipole moment, and ^r is the unit vector in the direction of →r.
At Point A (r, 0):
- The position vector →rA=(r,0).
- The unit vector ^rA=^i.
- The angle θA between →P and ^rA is 0∘.
Thus, the potential energy UA at point A is:
UA=kP⋅1r2=kPr2
At Point B (-r, 0):
- The position vector →rB=(−r,0).
- The unit vector ^rB=−^i.
- The angle θB between →P and ^rB is 180∘.
Thus, the potential energy UB at point B is:
UB=kP⋅(−1)r2=−kPr2
Step 3: Calculate the Work Done by the External Agent
The work done W by the external agent in moving the charge from point A to point B is equal to the change in potential energy:
W=UB−UA
Substituting the values we found:
W=(−kPr2)−(kPr2)=−kPr2−kPr2=−2kPr2
Step 4: Conclusion
The work done by the external agent is:
W=−2kPr2
We have an electric dipole fixed at the origin with its dipole moment →P directed along the positive x-direction. A positive charge is moved from point A(r,0) to point B(−r,0).
The electric potential V due to a dipole at a point →r is given by:
V=k→P⋅^rr2
where k is a constant, →P is the dipole moment, and ^r is the unit vector in the direction of →r.
- The position vector →rA=(r,0).
- The unit vector ^rA=^i.
- The angle θA between →P and ^rA is 0∘.
UA=kP⋅1r2=kPr2
- The position vector →rB=(−r,0).
- The unit vector ^rB=−^i.
- The angle θB between →P and ^rB is 180∘.
UB=kP⋅(−1)r2=−kPr2
The work done W by the external agent in moving the charge from point A to point B is equal to the change in potential energy:
W=UB−UA
Substituting the values we found:
W=(−kPr2)−(kPr2)=−kPr2−kPr2=−2kPr2
The work done by the external agent is:
W=−2kPr2
Similar Questions
An electric dipole is placed at origin in the xy plane with its orientation along the positive x-axis. The direction is electric field .
View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View SolutionA dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
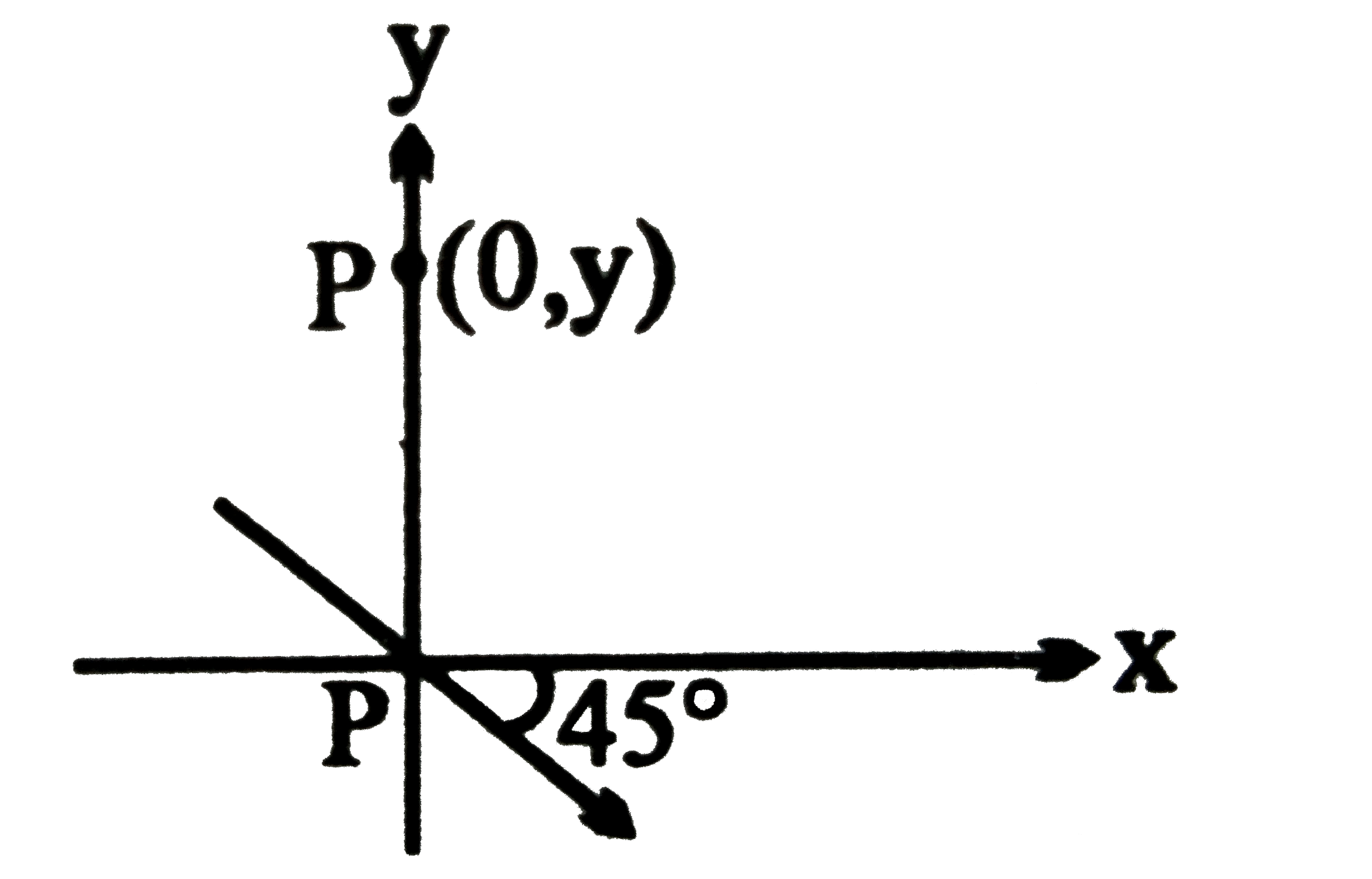 .
.
View SolutionA uniform electric field of magnitude 250V/m is directed in the positive x-direction. A+12μC charge moves from the origin to the point (x,y)=(20.0cm,5.0cm).
(a) What was the change in the potential energy of this charge?
(b) Through what potential difference did the charge move?
View SolutionAssertion: A small electric dipole is moved translatonally from higher potential to lower potential in uniform electric field. Work done by electric is positive.
Reason: When a positive charge is moved from higher potential to lower potential, work done by electric field positive.
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:

View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:

View SolutionMoment of a force of magnitude 20 N acting along positive x-direction at point (3m,0,0) about the point (0,2,0) (in N-m) is
View SolutionA negative charge is moved by an external agent in the direction of electric field. Then
 .
.
View SolutionA negetive charge is moved by an external agent in the direction of electric field. Then

View Solution
