A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
Constant in magnitude
Constant in direction
Constant in magnitude as well as direction
None of the above
The correct Answer is:A
To solve the problem, we need to analyze the motion of a point A on the surface of a circular disc that rolls without slipping along a horizontal surface with a constant velocity v0.
1. Understanding the Motion of the Disc:
- The disc rolls without slipping, which means that the point of contact with the ground (let's call it point P) is momentarily at rest.
- The disc has a radius R and rolls with a constant translational velocity v0.
2. Relating Translational and Rotational Motion:
- The angular velocity ω of the disc is related to the translational velocity v0 by the equation:
v0=Rω
- Since the disc rolls without slipping, the point A on the surface of the disc will have a velocity that is a combination of its translational motion and its rotational motion about point P.
3. Analyzing the Point A:
- Point A is located on the surface of the disc. As the disc rolls, point A will move in a circular path about point P.
- The acceleration of point A can be divided into two components:
- Tangential Acceleration: This is due to the change in the speed of point A along the circular path. Since the disc rolls with a constant velocity v0, the tangential acceleration is zero.
- Centripetal Acceleration: This is due to the circular motion of point A around point P. The centripetal acceleration ac is given by:
ac=v2R
- Here, v is the linear speed of point A, which is equal to v0 since point A is moving with the disc.
4. Calculating the Centripetal Acceleration:
- Substituting v=v0 into the centripetal acceleration formula:
ac=v20R
5. Conclusion:
- Since there is no tangential acceleration (the speed is constant), the total acceleration of point A is purely centripetal:
aA=v20R
Final Answer:
The acceleration of point A on the surface of the disc is:
aA=v20R
- The disc rolls without slipping, which means that the point of contact with the ground (let's call it point P) is momentarily at rest.
- The disc has a radius R and rolls with a constant translational velocity v0.
- The angular velocity ω of the disc is related to the translational velocity v0 by the equation:
v0=Rω
- Since the disc rolls without slipping, the point A on the surface of the disc will have a velocity that is a combination of its translational motion and its rotational motion about point P.
- Point A is located on the surface of the disc. As the disc rolls, point A will move in a circular path about point P.
- The acceleration of point A can be divided into two components:
- Tangential Acceleration: This is due to the change in the speed of point A along the circular path. Since the disc rolls with a constant velocity v0, the tangential acceleration is zero.
- Centripetal Acceleration: This is due to the circular motion of point A around point P. The centripetal acceleration ac is given by:
ac=v2R
- Here, v is the linear speed of point A, which is equal to v0 since point A is moving with the disc.
- Substituting v=v0 into the centripetal acceleration formula:
ac=v20R
- Since there is no tangential acceleration (the speed is constant), the total acceleration of point A is purely centripetal:
aA=v20R
The acceleration of point A on the surface of the disc is:
aA=v20R
Similar Questions

A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View SolutionA conducting disc of radius R is rolling without sliding on a horizontal surface with a constant velocity v.A uniform magnetic field of strength B is applied normal to the plane of the disc.Find the EMF induced between (at this moment )
(a)P&Q , (b)P&C , (c )Q&C
(C is centre P&Q are opposite points on vertical diameter of the disc)

View SolutionA wheel ( to be considered as a ring ) of mass m and radius R rolls without sliding on a horizontal surface with constant velocity v. It encounters a step of height R/2 at which it ascends without sliding
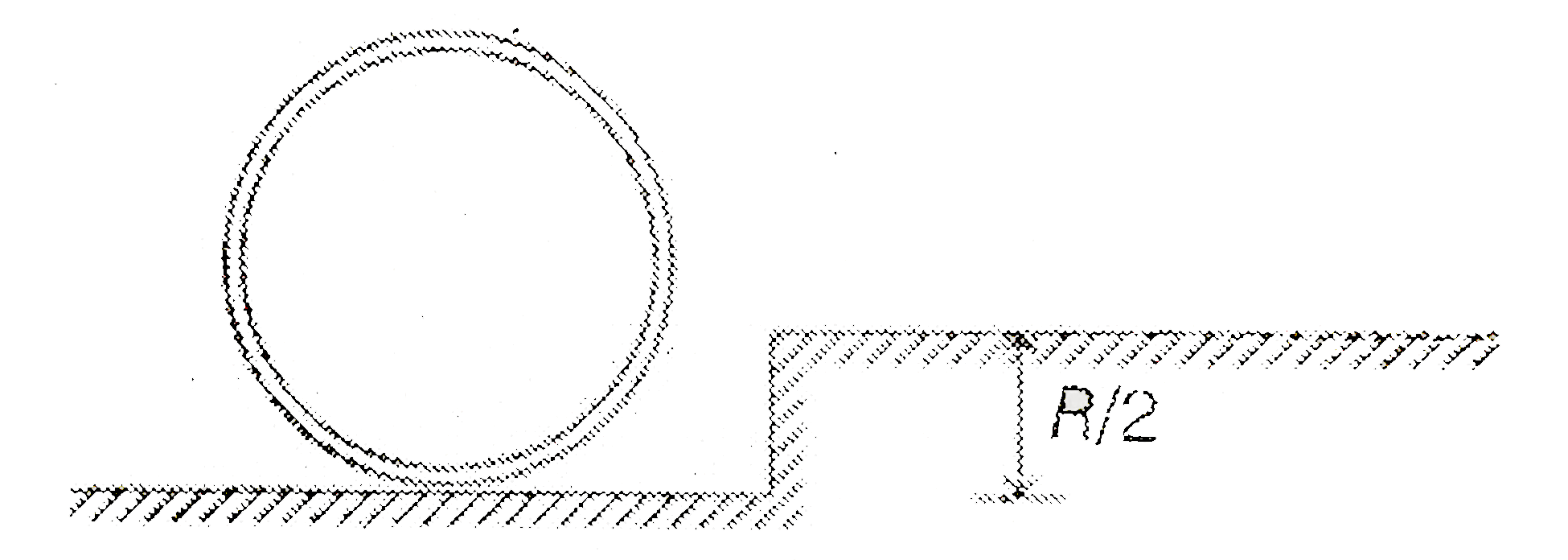
View Solution
A uniform circular ring rolls without slipping on a horizontal surface. At any instant, its position is as shown in the figure. Then
View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
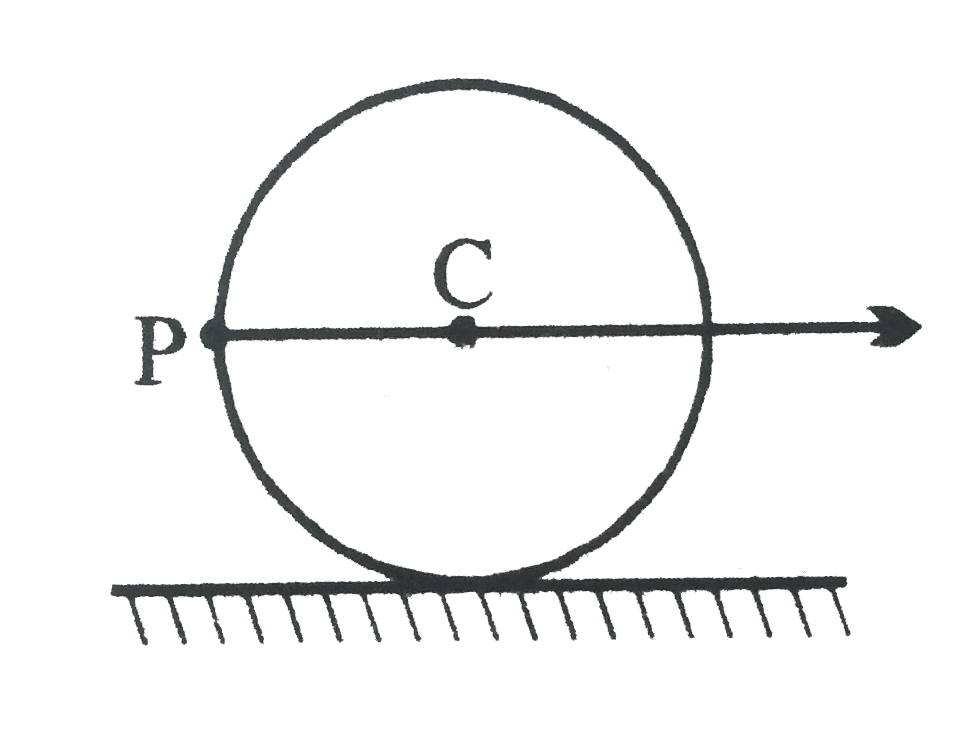 .
.
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View Solution