The pressure at the bottom of a tank of liquid is not proprtional to
Acceleration due to gravity
Density of the liquid
Height of the liquid
Area of the liquid surface
The correct Answer is:D
To solve the question regarding the pressure at the bottom of a tank of liquid and to determine which quantity it is not proportional to, we can follow these steps:
1. Understand the Concept of Pressure:
Pressure at a point in a fluid at rest is defined as the force exerted per unit area. The formula for pressure (P) is given by:
P=FA
where F is the force and A is the area.
2. Identify the Force Acting on the Liquid:
The force exerted at the bottom of the tank is due to the weight of the liquid above it. The weight (W) of the liquid can be expressed as:
W=m⋅g
where m is the mass of the liquid and g is the acceleration due to gravity.
3. Express Mass in Terms of Density and Volume:
The mass of the liquid can be expressed in terms of its density (ρ) and volume (V):
m=ρ⋅V
The volume of the liquid in the tank can be calculated as:
V=A⋅h
where A is the cross-sectional area of the tank and h is the height of the liquid column.
4. Combine the Equations:
Substituting the expression for volume into the weight equation gives:
W=ρ⋅(A⋅h)⋅g
5. Calculate Pressure at the Bottom of the Tank:
Now substituting the expression for weight into the pressure formula:
P=WA=ρ⋅(A⋅h)⋅gA
Simplifying this, we get:
P=ρ⋅h⋅g
6. Analyze the Proportionality:
From the final expression P=ρ⋅h⋅g, we can see that pressure is directly proportional to:
- Density (ρ)
- Height (h)
- Acceleration due to gravity (g)
However, pressure is not proportional to the area (A) of the tank since the area cancels out in the calculation.
Conclusion:
The pressure at the bottom of a tank of liquid is not proportional to the area of the liquid.
Pressure at a point in a fluid at rest is defined as the force exerted per unit area. The formula for pressure (P) is given by:
P=FA
where F is the force and A is the area.
The force exerted at the bottom of the tank is due to the weight of the liquid above it. The weight (W) of the liquid can be expressed as:
W=m⋅g
where m is the mass of the liquid and g is the acceleration due to gravity.
The mass of the liquid can be expressed in terms of its density (ρ) and volume (V):
m=ρ⋅V
The volume of the liquid in the tank can be calculated as:
V=A⋅h
where A is the cross-sectional area of the tank and h is the height of the liquid column.
Substituting the expression for volume into the weight equation gives:
W=ρ⋅(A⋅h)⋅g
Now substituting the expression for weight into the pressure formula:
P=WA=ρ⋅(A⋅h)⋅gA
Simplifying this, we get:
P=ρ⋅h⋅g
From the final expression P=ρ⋅h⋅g, we can see that pressure is directly proportional to:
- Density (ρ)
- Height (h)
- Acceleration due to gravity (g)
The pressure at the bottom of a tank of liquid is not proportional to the area of the liquid.
Similar Questions
The pressure at the bottom of a tank of water is 2P, where P is the atmospheric pressure.If the water is drawn out till the level of water is lowered by one half of initial,the pressure at the bottom of the tank will now be
View SolutionThe pressure at the bottom of an open tank of water is 3p where p is the atmospheric pressure. If the water is drawn out till the level of water remains one fifth, the pressure at the bottom of the tank will now be
View SolutionP is the atmospheric pressure and the pressure at the bottom of a tank of water is 3P. If the water is drawn out to lower the level of water by one fifth, then the pressure at the bottom of the tank will be
View SolutionThe pressure at the bottom of a liquid container is determined by the
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View SolutionThe pressure at the bottom of a water tank is 4 P, where P is .atmospheric pressure. If water is drawn out till the water level decreases by —35th, then pressure at the bottom of the tank is
View SolutionAssertion : The solubility of a gas in a liquid increases with increase of pressure.
Reason : The solubility of a gas in a liquid is directly proportional to the pressure of the gas.
View SolutionA hole is made at the bottom of the tank filled with water (density =1000kgm−3). If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere =105Nm−2), then the velocity of efflux is nearest to
View SolutionIf the gauge pressure, at the bottom of a water tank is 2.7 kPa, what is the height of the water [Take g = 10 m s−2]
Hint : Gauge Pressure = absolute pressure - atmospheric pressure = pgh
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
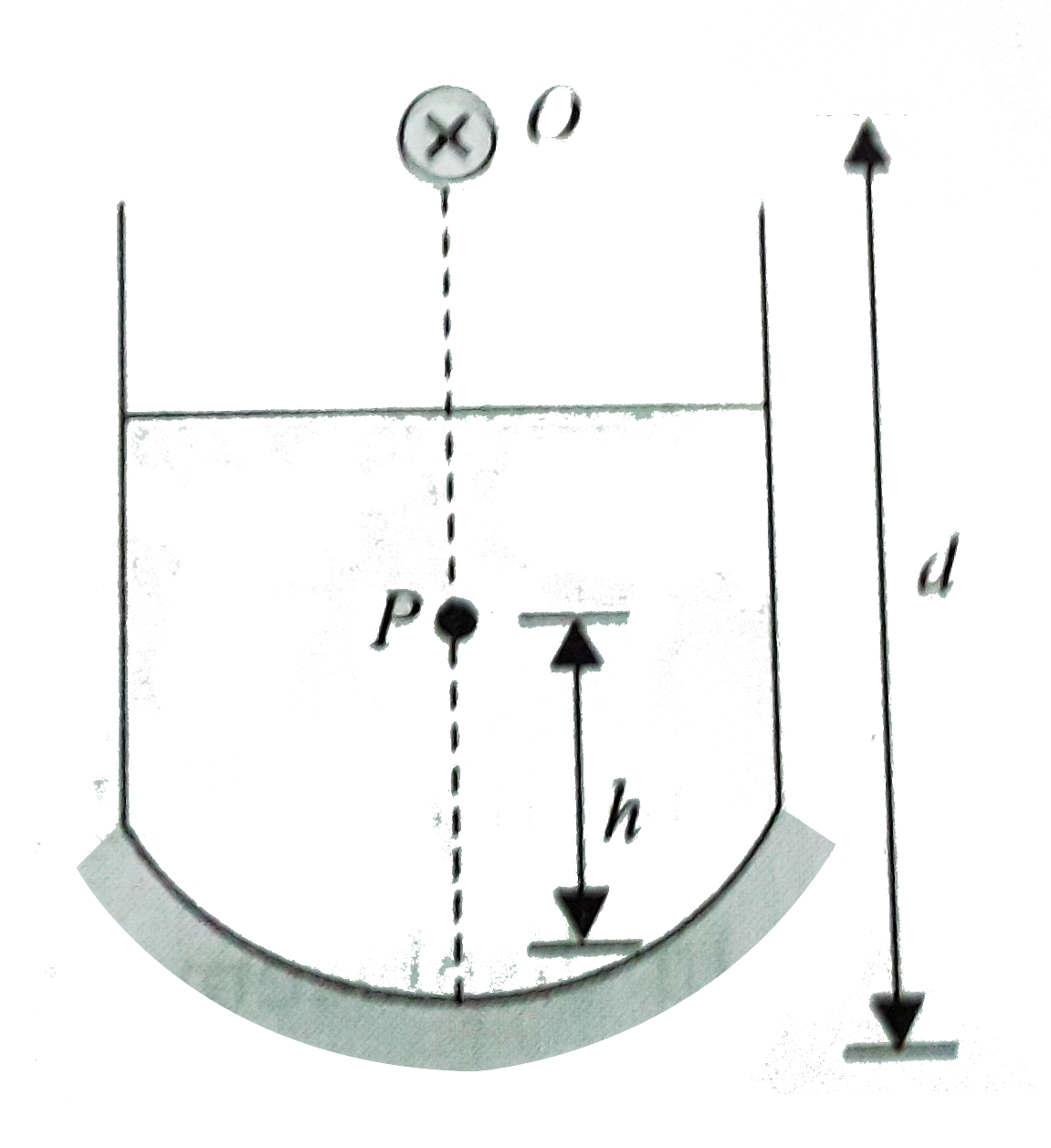
View Solution