A metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
YAαT1−αT
YAαT1+αT
1−αTYAαT
(1+αT)YAαT
The correct Answer is:B
To find the force required to prevent the expansion of a metal rod of length L and cross-sectional area A when heated through T degrees Celsius, we can follow these steps:
Step 1: Understand the Thermal Expansion
When the rod is heated, it expands. The increase in length ΔL due to thermal expansion can be expressed as:
ΔL=αLT
where α is the coefficient of linear expansion of the material.
Step 2: Determine the New Length
The new length L′ of the rod after heating can be expressed as:
L′=L+ΔL=L+αLT=L(1+αT)
Step 3: Apply Compressive Force
To prevent the rod from expanding, we need to apply a compressive force F. This force will create a compressive stress in the rod, which can be expressed as:
Stress=FA
Step 4: Relate Stress to Strain
According to Hooke's Law, the stress is also related to strain by Young's modulus Y:
Stress=Y×Strain
The strain Strain can be defined as:
Strain=ΔLL′
Substituting ΔL=αLT and L′=L(1+αT):
Strain=αLTL(1+αT)=αT1+αT
Step 5: Set Up the Equation
Now, we can equate the expressions for stress:
FA=Y×αT1+αT
Step 6: Solve for the Force F
Rearranging the equation to solve for the force F:
F=AY×αT1+αT
Final Expression
Thus, the force required to prevent the expansion of the rod lengthwise is:
F=AYαT1+αT
When the rod is heated, it expands. The increase in length ΔL due to thermal expansion can be expressed as:
ΔL=αLT
where α is the coefficient of linear expansion of the material.
The new length L′ of the rod after heating can be expressed as:
L′=L+ΔL=L+αLT=L(1+αT)
To prevent the rod from expanding, we need to apply a compressive force F. This force will create a compressive stress in the rod, which can be expressed as:
Stress=FA
According to Hooke's Law, the stress is also related to strain by Young's modulus Y:
Stress=Y×Strain
The strain Strain can be defined as:
Strain=ΔLL′
Substituting ΔL=αLT and L′=L(1+αT):
Strain=αLTL(1+αT)=αT1+αT
Now, we can equate the expressions for stress:
FA=Y×αT1+αT
Rearranging the equation to solve for the force F:
F=AY×αT1+αT
Thus, the force required to prevent the expansion of the rod lengthwise is:
F=AYαT1+αT
Similar Questions
Calculate the compressional force required to prevent the metallic rod length lcm and cross-sectional area Acm2 when heated through t∘C, from expanding along length wise. The Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree Celsius
View SolutionA steel rod of length 25cm has a cross-sectional area of 0.8cm2 . The force required to stretch this rod by the same amount as the expansion produced by heating it through 10∘C is (αsteel=10−5/∘C and Ysteel=2×1010N/m2)
View SolutionCalculate the compressional force required to prevent the metallic rod of length l cm and cross sectional area Acm2 when heated through t∘C from expanding lengthwise. Young's modulus of elasticity of the metal is E and mean coefficient of linear expansion is α per degree celsius.
View SolutionA metal rod of length 100cm, made of silver at 0∘C is heated to 100∘C . It's length is increased by 0.19cm . Coefficient of cubical expansion of the silver rod is
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod is
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
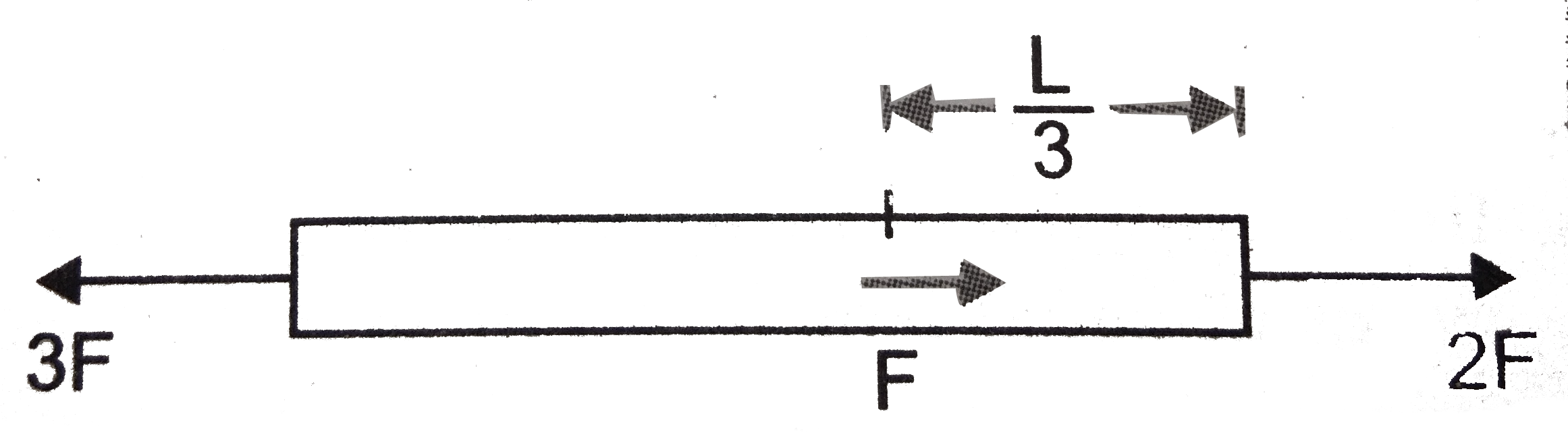
View SolutionA steel rod (Y=2.0×1011N/m2 and α=10−50.∘C−1) of length 1 m and area of cross-section 1 cm2 is heated from 0.∘C to 200∘C, without being allowed to extend or bend. What is the tension produced in the rod?
View SolutionA metallic rod l cm long, A square cm in cross-section is heated through t∘C. If Young’s modulus of elasticity of the metal is E and the mean coefficient of linear expansion is α per degree celsius, then the compressional force required to prevent the rod from expanding along its length is
View SolutionA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View Solution