The gas inside a spherical bubble expands uniformly and slowly so that its radius increases from R to 2R. Let the atmospheric pressure be p0 and surface tension be S. The work done by the gas in the process is
28πR3P03+24πsR2
25πR3P03+24πsR2
25πR3P03+23πsR22
23πR2
The correct Answer is:A
To find the work done by the gas in expanding from a radius R to 2R in a spherical bubble, we need to consider both the work done against the atmospheric pressure and the work done against the surface tension of the bubble.
1. Identify the Work Done Against Atmospheric Pressure:
The work done by the gas against the atmospheric pressure p0 when the radius increases from R to 2R can be expressed as:
Wpressure=∫2RR4πr2p0dr
Here, 4πr2 is the surface area of the bubble, and p0 is the atmospheric pressure.
2. Calculate the Work Done Against Surface Tension:
The work done against the surface tension S is given by:
Wsurface=∫2RR4Sdr
The factor 4S comes from the fact that the surface area increases as the bubble expands.
3. Combine the Work Done:
The total work done by the gas during this process is the sum of the work done against pressure and surface tension:
Wtotal=Wpressure+Wsurface
4. Perform the Integration:
- For the work done against atmospheric pressure:
Wpressure=4πp0∫2RRr2dr=4πp0(r33)2RR=4πp0((2R)33−R33)
=4πp0(8R3−R33)=4πp0(7R33)=28πp0R33
- For the work done against surface tension:
Wsurface=4S∫2RRdr=4S(r)2RR=4S(2R−R)=4SR
5. Final Expression for Total Work Done:
Combining both contributions:
Wtotal=28πp0R33+4SR
Final Answer:
The total work done by the gas in the process is:
W=28πp0R33+4SR
The work done by the gas against the atmospheric pressure p0 when the radius increases from R to 2R can be expressed as:
Wpressure=∫2RR4πr2p0dr
Here, 4πr2 is the surface area of the bubble, and p0 is the atmospheric pressure.
The work done against the surface tension S is given by:
Wsurface=∫2RR4Sdr
The factor 4S comes from the fact that the surface area increases as the bubble expands.
The total work done by the gas during this process is the sum of the work done against pressure and surface tension:
Wtotal=Wpressure+Wsurface
- For the work done against atmospheric pressure:
Wpressure=4πp0∫2RRr2dr=4πp0(r33)2RR=4πp0((2R)33−R33)
=4πp0(8R3−R33)=4πp0(7R33)=28πp0R33
Wsurface=4S∫2RRdr=4S(r)2RR=4S(2R−R)=4SR
Combining both contributions:
Wtotal=28πp0R33+4SR
The total work done by the gas in the process is:
W=28πp0R33+4SR
Similar Questions
A gas expands from 75 liter to 125 liter at a constant pressure of 4 atmosphere. If one atmospheric pressure is 1.0x105Pa(Nm−2), calculate the work done by the gas during this expansion.
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View Solution
Knowledge Check
The temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure P=aT−1 where a is a constant .Then the work done by the gas is
Aa. nRTBb. 4nRTCc. 2nRTDd. 6nRT
The internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
The heat absorbed by the gas in the process is
View SolutionAir is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution is S, the work done in the process is
View SolutionA small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).
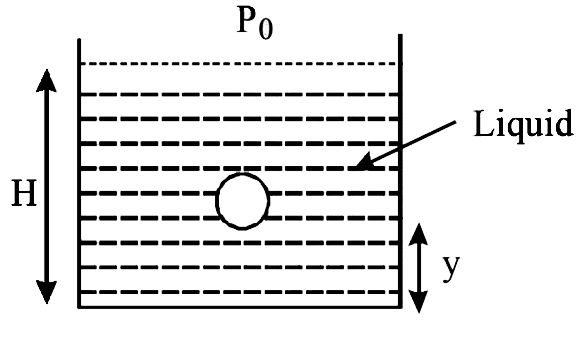
The buoyancy force acting on the gas bubble is (Assume R is the universal gas constant)
View SolutionA small spherical monoatomic ideal gas bubble (γ=53) is trapped inside a liquid of density ρl (see figure) . Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
_E01_434_Q01.png)
When the gas bubble is at a height y from the bottom , its temperature is :-
View SolutionFor gaseous reactions, if ΔH is the change in enthalpy and ΔU that in internal energy, then
View SolutionThe amount of work done in blowing a soap bubble such that its diameter increases from d to D is (T=surface tension of the solution)
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View Solution