The coefficient of friction between two surface is μ=0.8. The tension in the string as shown in the figure is
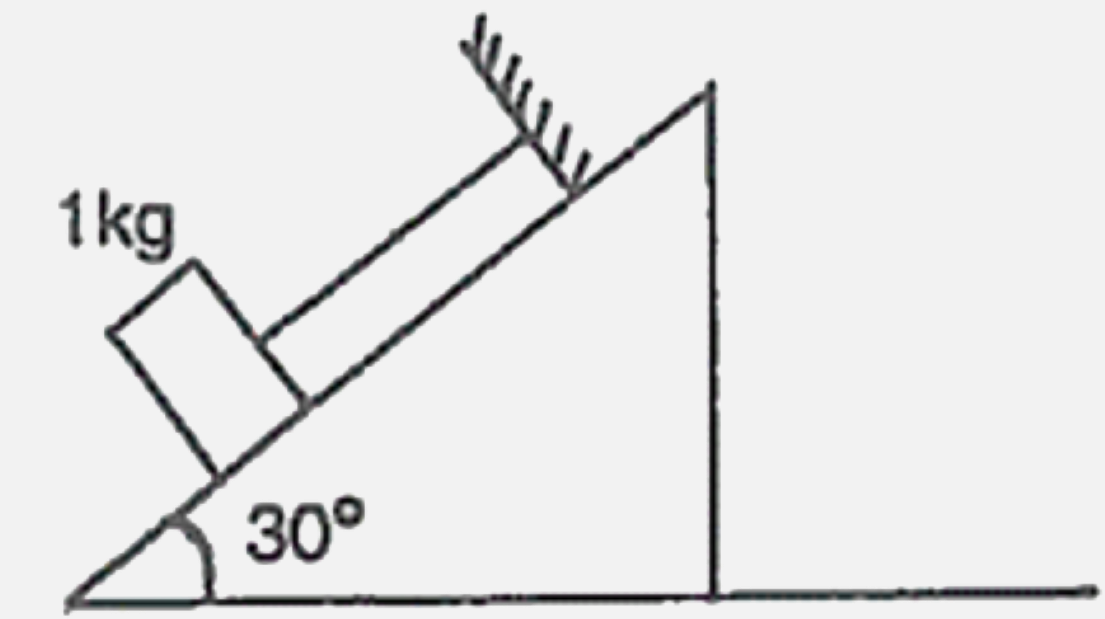
0 N
6 N
4 N
8 N
The correct Answer is:A
Step by step video & image solution for The coefficient of friction between two surface is mu= 0.8. The tension in the string as shown in the figure is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The tension T in the string shown in figure is

View SolutionThe coefficient of static friction between two surfaces depend on
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View SolutionFind the tension in the strings AC and BC shown in figure.

View SolutionThe coefficient of static friction, μs between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless.(g=10m/s2)

View SolutionThe coefficient of friction between the two two blocks is 0.3 where as the surface AB is smooth

View SolutionThe coefficient of static friction, μs between block A mass 2kg and the table as shown in the figure, is 0.2. What would be the maximum mass value of block B, so that the two blocks do not move ? The string and the pulley are asseumed to be smooth and massless (g=10m/s2)

View SolutionWhat is the acceleration of the block and trolley system shown in if the coefficient of kinetic friction between the trolley and the surface is 0 .04 ? What is the tension in the string ? Take g=10ms−2 Neglect the mass of the string
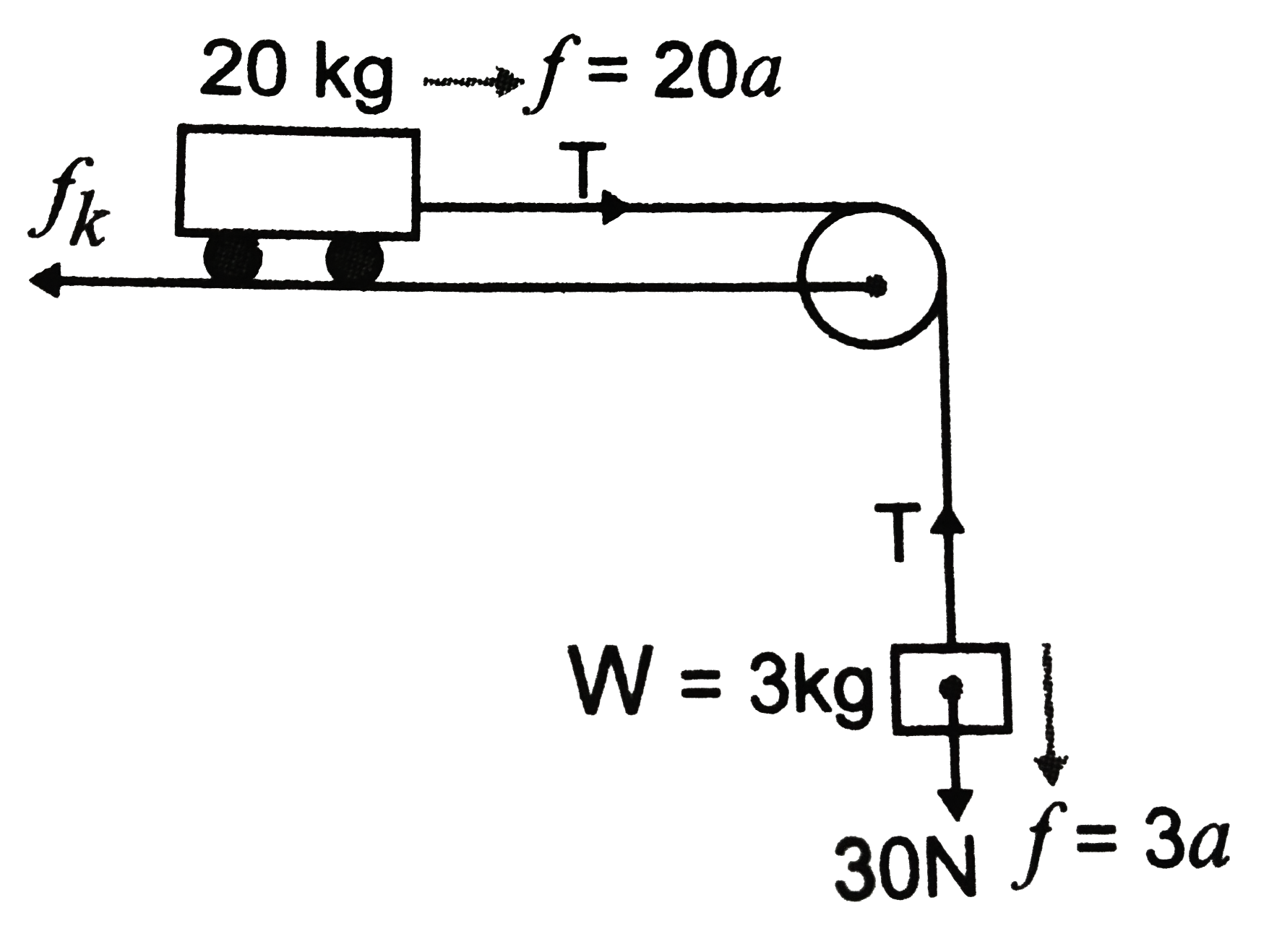 .
.
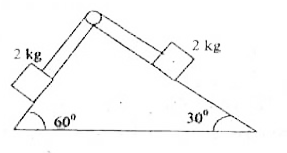
View SolutionOn the figure shown two blocks each of mass 2 kg are connected though a massless inextensible string, which posses over a frictionless pulley. The coefficient of friction between any two surface is μ=0.1. Find the acceleration of the blocks.
View SolutionTwo uniform boards, tied together with the help of a string, are balanced on a surface as shown in Fig.
The coefficient of static friction between boards and surface is 0.5. The minimum value of θ, for which this type of arrangement is possible is

View Solution
