When a resistor of 11Ω is connected in series with an electric cell, the current following in it is 0.5A. Instead, when a resistor of 5Ω is connected to the same electric cell in series, the current increases by 0.4A The internal resistance of the cell is
1.5Ω
2Ω
2.5Ω
3.5Ω
The correct Answer is:C
To find the internal resistance of the cell, we can follow these steps:
Step 1: Set up the equations for the two scenarios
1. First scenario: When a resistor of 11 Ω is connected, the current is 0.5 A.
- Let V be the voltage of the cell and r be the internal resistance of the cell.
- The total resistance in the circuit is R+r=11+r.
- Using Ohm's law, we can write:
I1=VR+r⟹0.5=V11+r(Equation 1)
2. Second scenario: When a resistor of 5 Ω is connected, the current increases by 0.4 A, making the new current 0.9 A.
- The total resistance in this case is R+r=5+r.
- Again using Ohm's law:
I2=VR+r⟹0.9=V5+r(Equation 2)
Step 2: Solve the equations for V
From Equation 1:
V=0.5(11+r)=5.5+0.5r(1)
From Equation 2:
V=0.9(5+r)=4.5+0.9r(2)
Step 3: Set the two expressions for V equal to each other
Since both expressions represent V, we can set them equal:
5.5+0.5r=4.5+0.9r
Step 4: Rearrange the equation to solve for r
Rearranging gives:
5.5−4.5=0.9r−0.5r
1=0.4r
Step 5: Solve for r
Dividing both sides by 0.4:
r=10.4=2.5Ω
Conclusion
The internal resistance of the cell is 2.5Ω.
---
- Let V be the voltage of the cell and r be the internal resistance of the cell.
- The total resistance in the circuit is R+r=11+r.
- Using Ohm's law, we can write:
I1=VR+r⟹0.5=V11+r(Equation 1)
- The total resistance in this case is R+r=5+r.
- Again using Ohm's law:
I2=VR+r⟹0.9=V5+r(Equation 2)
V=0.5(11+r)=5.5+0.5r(1)
V=0.9(5+r)=4.5+0.9r(2)
5.5+0.5r=4.5+0.9r
5.5−4.5=0.9r−0.5r
1=0.4r
r=10.4=2.5Ω
Similar Questions
Three resistors of 2Ω,3Ω and 4Ω are connected in
series
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionA cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate :
the internal resistance,
View SolutionAs electric lamp and a conductor of resistance 4Ω are connected in series to a 6 V battery. The current drawn by the lamp is 0.25 A. Find the resistance of the electric lamp.
View SolutionAn ideal battery sends a current of 5A in a resistor. When another resistor of value 10Ω is connected in parallel ,the current through the battery is increased to 6A.Find the resistance of the first resistor.
View SolutionWhen a resistance of 2 ohm is connected across terminals of a cell, the current is 0.5A. When the resistance is increased to 5 ohm, the current is 0.25A The e.m.f. of the cell is
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
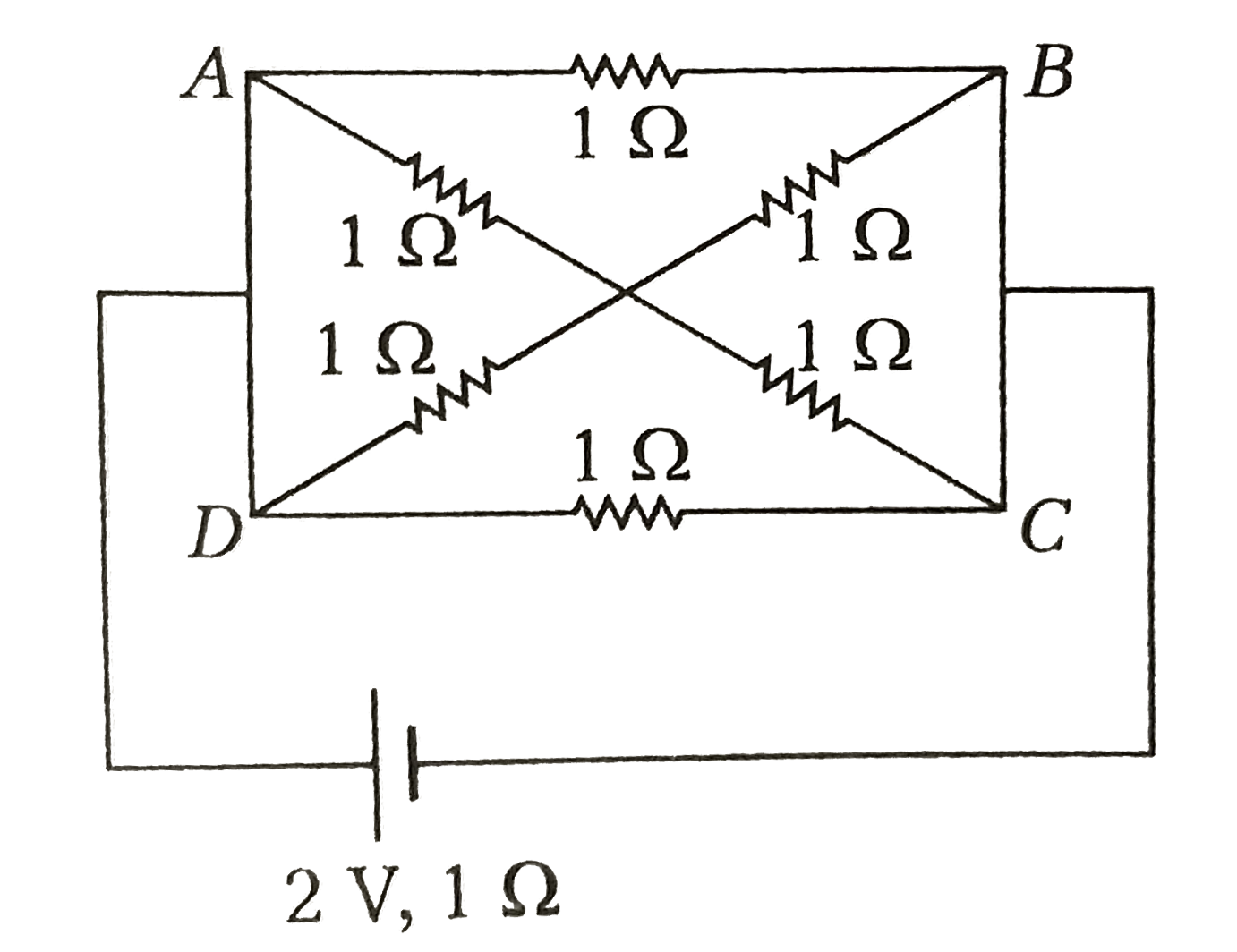
View SolutionA cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate :
e.m.f. of the cell.
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View Solution
