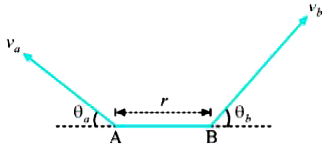
A wave pulse is generated in a string that lies along x- axis. At the points A and B, as shown in the figure, if RAandRB are the ratio of wave speed to the particle speed respectively then:
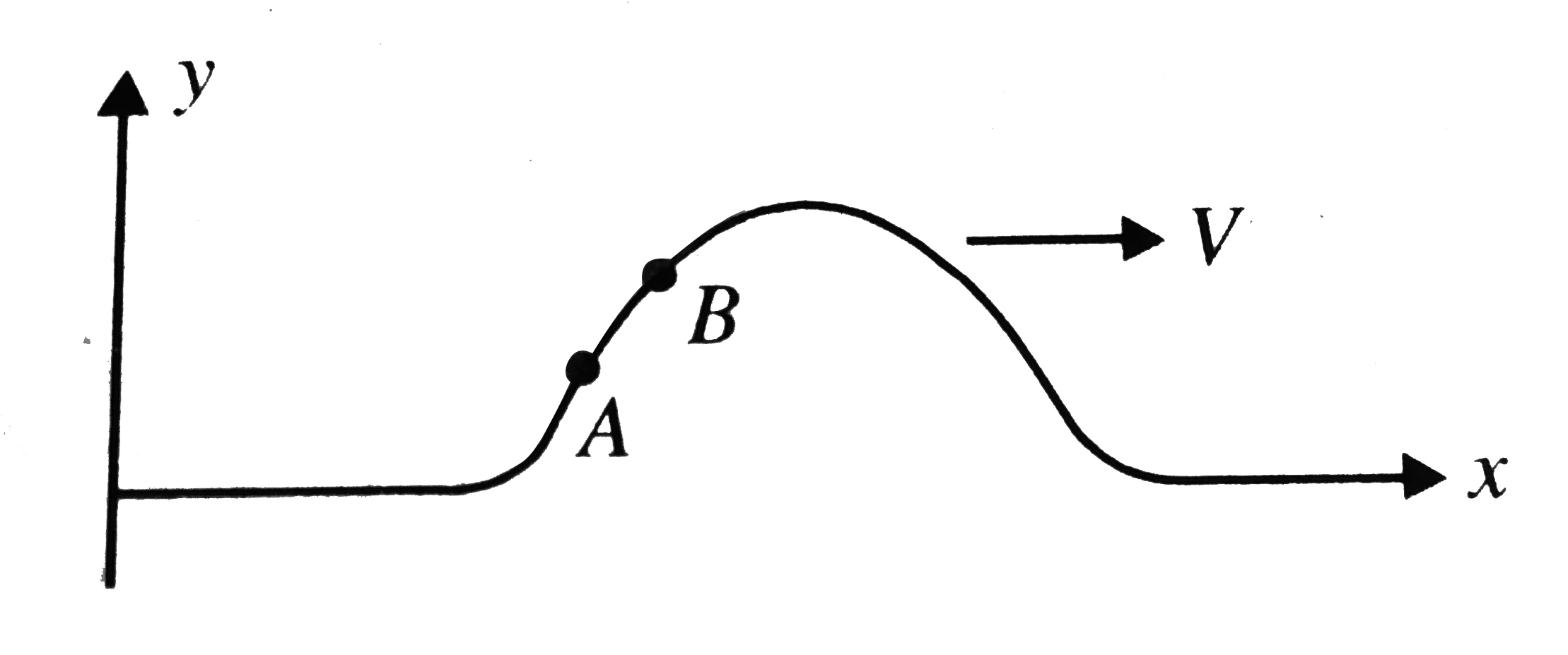
RA>RB
RB>RA
RA=RB
Information is not sufficient to decide.
The correct Answer is:B
Step by step video & image solution for A wave pulse is generated in a string that lies along x- axis. At the points A and B, as shown in the figure, if R_A and R_B are the ratio of wave speed to the particle speed respectively then: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A wave pulse is generated in a string that lies along x−axis. At the points A and B, as shown in figure, if RA and RB are ratio of magnitudes of wave speed to the particle speed, then

View SolutionA string of mass m and length l is hanging from ceiling as shown in the Fig. Wave in string move upward. vAand vB are the speed of wave at A and B respectively. Then vBis :
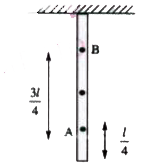
View Solution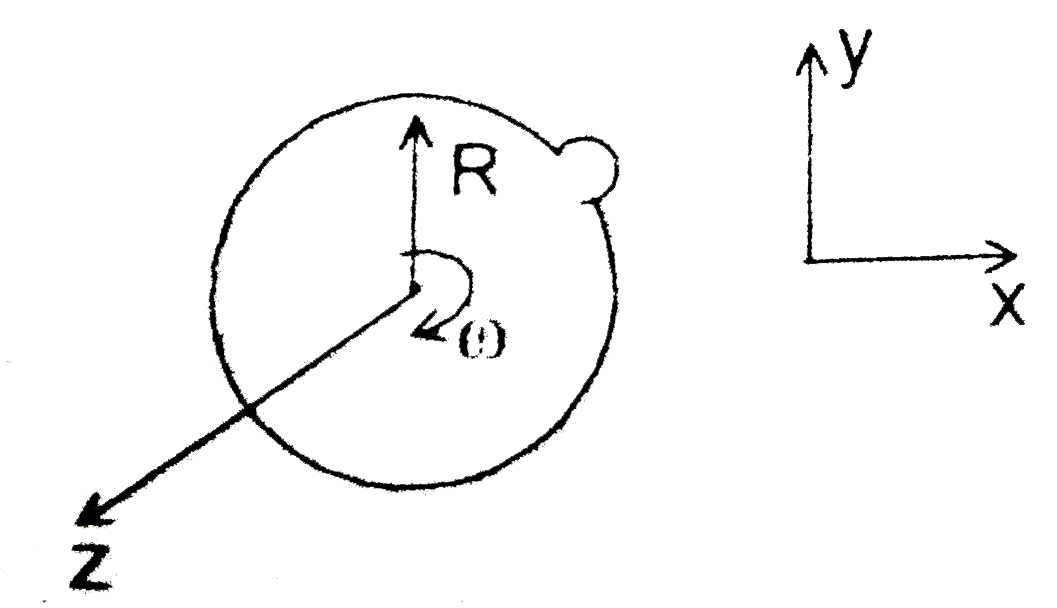
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.
View SolutionA system is as shown in the figure. All speeds shown are with respect to ground. Then the speed of Block B with respect to ground is :
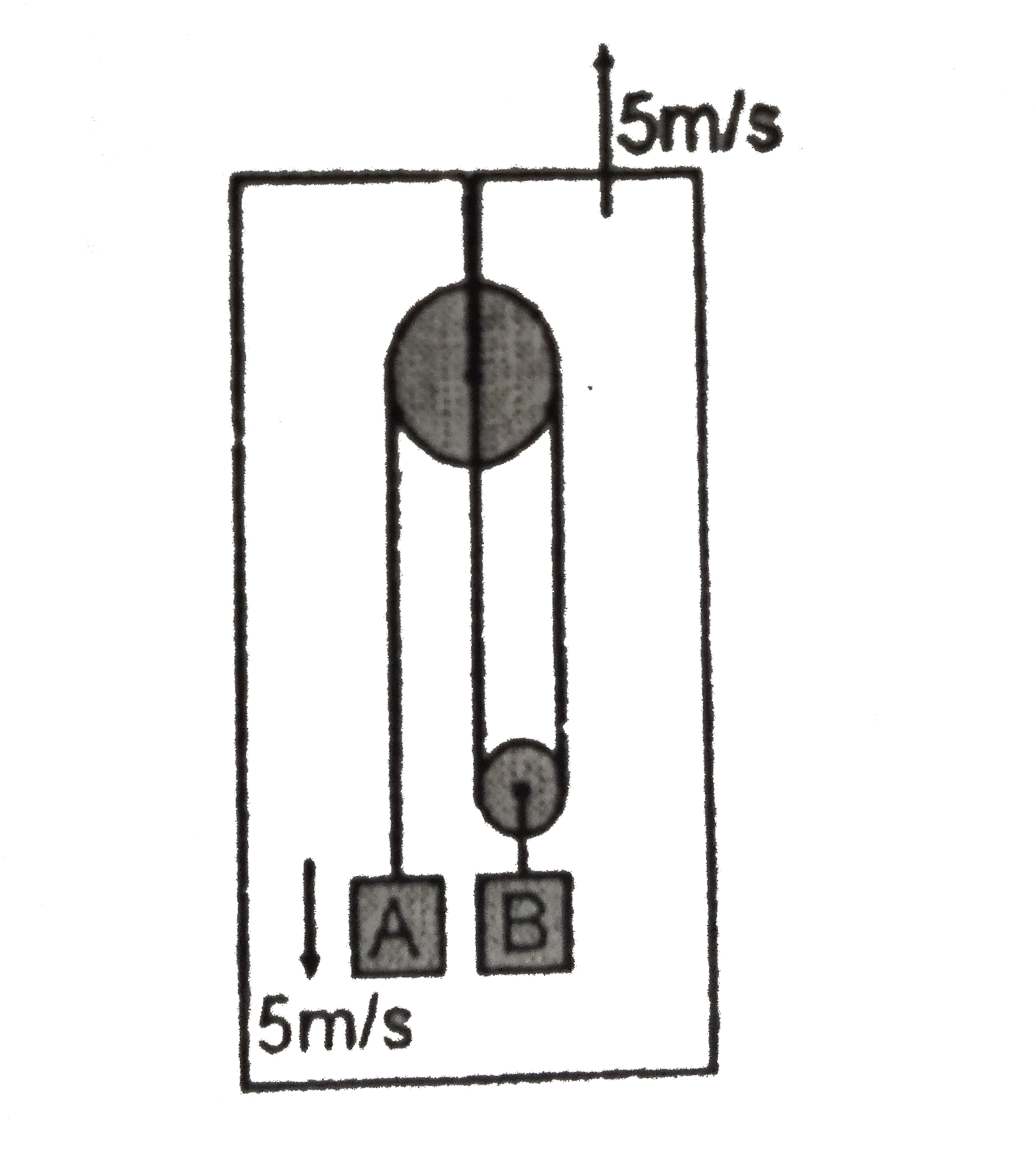
View SolutionA transverse wave travels along x-axis . The particles of medium move
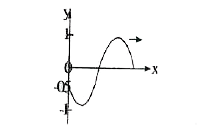
View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by

View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionTwo particles A and B are moving as shown in figure. At this moment of time, the angular speed of A with respect to B is?
View SolutionIf the equation of a travelling wave is given as y = 40 cos (1600t + 6x), (where y is in millimeter, t is in second and x is in meter), then ratio of the wave speed to the maximum particle speed will be
View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by
View Solution
