The ratio of magnetic fields due to a bar magnet at the two axial points P1andP2 which are separated from each other by 10 cm is 25 :2 . Point P1 is situated at 10 cm from the centre of the magnet. Magnetic length of the bar magnet is (Points P1andP2 are on the same side of magnet and distance of P2 from the centre is greater than distance of P1 from the centre of magnet)
5 cm
10 cm
15 cm
20 cm
The correct Answer is:B
To solve the problem, we need to find the magnetic length of a bar magnet given the ratio of magnetic fields at two axial points P1 and P2 and their respective distances from the center of the magnet.
1. Identify the Given Information:
- Ratio of magnetic fields at points P1 and P2: B1B2=252
- Distance between P1 and P2: 10cm
- Distance of P1 from the center of the magnet: d1=10cm
- Therefore, distance of P2 from the center of the magnet: d2=d1+10=20cm
2. Magnetic Field Formula:
The magnetic field B at an axial point from a bar magnet is given by:
B=μ04π⋅2md3
where m is the magnetic moment of the magnet and d is the distance from the center.
3. Write the Equations for B1 and B2:
- For point P1:
B1=μ04π⋅2m(10)3=μ04π⋅2m1000
- For point P2:
B2=μ04π⋅2m(20)3=μ04π⋅2m8000
4. Set Up the Ratio:
Using the ratio given:
B1B2=2m10002m8000=80001000=8
However, we know from the problem statement that:
B1B2=252
Therefore, we can equate:
8=252
5. Equate the Two Ratios:
From the above, we can set up the equation:
80001000=252
Cross-multiplying gives:
16000=2500
This indicates that we need to consider the lengths involved.
6. Using the Length of the Magnet:
Let l be the half-length of the magnet. The magnetic field equations will also depend on l:
B1=μ04π⋅2m(10)3−l2
B2=μ04π⋅2m(20)3−l2
7. Set Up the Ratio Again:
B1B2=(203−l2)(103−l2)=252
Substituting 203=8000 and 103=1000:
8000−l21000−l2=252
8. Cross-Multiply and Solve for l2:
Cross-multiplying gives:
2(8000−l2)=25(1000−l2)
Expanding:
16000−2l2=25000−25l2
Rearranging gives:
23l2=9000⟹l2=900023
9. Calculate l:
l≈√391.3043≈19.78cm
Therefore, the total length L=2l≈39.56cm.
Final Answer:
The magnetic length of the bar magnet is approximately 39.56cm.
- Ratio of magnetic fields at points P1 and P2: B1B2=252
- Distance between P1 and P2: 10cm
- Distance of P1 from the center of the magnet: d1=10cm
- Therefore, distance of P2 from the center of the magnet: d2=d1+10=20cm
The magnetic field B at an axial point from a bar magnet is given by:
B=μ04π⋅2md3
where m is the magnetic moment of the magnet and d is the distance from the center.
- For point P1:
B1=μ04π⋅2m(10)3=μ04π⋅2m1000
- For point P2:
B2=μ04π⋅2m(20)3=μ04π⋅2m8000
Using the ratio given:
B1B2=2m10002m8000=80001000=8
However, we know from the problem statement that:
B1B2=252
Therefore, we can equate:
8=252
From the above, we can set up the equation:
80001000=252
Cross-multiplying gives:
16000=2500
This indicates that we need to consider the lengths involved.
Let l be the half-length of the magnet. The magnetic field equations will also depend on l:
B1=μ04π⋅2m(10)3−l2
B2=μ04π⋅2m(20)3−l2
B1B2=(203−l2)(103−l2)=252
Substituting 203=8000 and 103=1000:
8000−l21000−l2=252
Cross-multiplying gives:
2(8000−l2)=25(1000−l2)
Expanding:
16000−2l2=25000−25l2
Rearranging gives:
23l2=9000⟹l2=900023
l≈√391.3043≈19.78cm
Therefore, the total length L=2l≈39.56cm.
The magnetic length of the bar magnet is approximately 39.56cm.
Similar Questions
The ratio of the magnetic fields due to small bar magnet in end position an broad side on position is (at equal distance from the magnet)
View SolutionThe field due to a magnet at a distance R~ from the centre of the magnet is proportional
View SolutionFind the magnetic field at P due to the arrangement shown
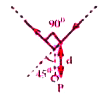
View SolutionFind the magnetic field at P due to the arrangement shown
 .
.
View SolutionThe ratio of the magnetic fields due to small bar magnet in end position and on broad side position is (at equal distance from the magnet)
View SolutionThe dipole moment of a short bar magnet is 1.25A−m2. The magnetic field on its axis at a distance of 0.5 metre from the centre of the magnet is
View SolutionThe magnetic field on the axis at a distance z from the centre of the bar magnet would be ?
View SolutionA long bar magnet has a pole strength of 10Am. Find the magnetic field at a point on the axis of the magnet at a distance of 5cm from the north pole of the magnet.
View SolutionDerive an expression for the magnetic field at a point on the axis located at a distance x from the centre of a magnetic dipole of length 2l and magnetic moment M.
View SolutionThe magnetic field at a point x on the axis of a small bar magnet is equal to the field at a point y on the equator of the same magnet. The ratio of the distances of x and y from the centre of the magnet is
View Solution
