A body of density d is counterpoised by Mg of weights of density d1 in air of density d. Then the true mass of the body is
M
M(1−dd2)
M(1−dd1)
M⎛⎜⎝1−dd21−dd1⎞⎟⎠
The correct Answer is:D
To solve the problem step by step, we need to analyze the forces acting on the body when it is submerged in air and counterpoised by another mass.
1. Understanding the Problem:
- We have a body with density d and mass m0.
- This body is counterpoised by another mass m of density d1 in air, which has a density d.
- We need to find the true mass m0 of the body.
2. Buoyant Force Calculation:
- When the body is submerged in air, it experiences a buoyant force. The buoyant force Fb can be calculated using Archimedes' principle:
Fb=density of air×volume of the body×g
- The volume V of the body can be expressed as:
V=m0d
- Therefore, the buoyant force becomes:
Fb=d×m0d×g=m0g
3. Apparent Weight Calculation:
- The apparent weight Wa of the body in air is given by:
Wa=true weight−buoyant force=m0g−Fb
- Substituting the buoyant force:
Wa=m0g−m0g=0
- This indicates that the body is in equilibrium with the counterpoised mass.
4. Equating Apparent Weights:
- The apparent weight of the body must equal the apparent weight of the counterpoised mass m of density d1:
mg−F′b=0
- The buoyant force on the counterpoised mass can be calculated similarly:
F′b=d×md1×g
- Thus, we have:
mg−d×md1×g=0
5. Setting Up the Equation:
- Since both apparent weights are equal, we can write:
m0g−d×m0d×g=mg−d×md1×g
- Canceling g from both sides:
m0−m0dd=m−mdd1
6. Solving for True Mass:
- Rearranging gives:
m0(1−dd1)=m(1−dd2)
- Therefore, the true mass m0 can be expressed as:
m0=m(1−dd2)(1−dd1)
Final Answer:
The true mass of the body is:
m0=m(1−dd2)(1−dd1)
- We have a body with density d and mass m0.
- This body is counterpoised by another mass m of density d1 in air, which has a density d.
- We need to find the true mass m0 of the body.
- When the body is submerged in air, it experiences a buoyant force. The buoyant force Fb can be calculated using Archimedes' principle:
Fb=density of air×volume of the body×g
- The volume V of the body can be expressed as:
V=m0d
- Therefore, the buoyant force becomes:
Fb=d×m0d×g=m0g
- The apparent weight Wa of the body in air is given by:
Wa=true weight−buoyant force=m0g−Fb
- Substituting the buoyant force:
Wa=m0g−m0g=0
- This indicates that the body is in equilibrium with the counterpoised mass.
- The apparent weight of the body must equal the apparent weight of the counterpoised mass m of density d1:
mg−F′b=0
- The buoyant force on the counterpoised mass can be calculated similarly:
F′b=d×md1×g
- Thus, we have:
mg−d×md1×g=0
- Since both apparent weights are equal, we can write:
m0g−d×m0d×g=mg−d×md1×g
- Canceling g from both sides:
m0−m0dd=m−mdd1
- Rearranging gives:
m0(1−dd1)=m(1−dd2)
- Therefore, the true mass m0 can be expressed as:
m0=m(1−dd2)(1−dd1)
The true mass of the body is:
m0=m(1−dd2)(1−dd1)
Similar Questions
The weight of a body in water is one third of its weight in air. The density of the body is
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionA light cylindrical tube 'T' of length l and radius 'r' containing air is inverted in water (density d). One end of the tube is open and the other is closed A block 'B' of density 2d is kept on the tube as shown in the figure. The tube stays in equilibrium in the position shown. (Assume the atmosphere pressure is to be P0)
Assume that density of air is very small than density of block and water. Pick up the correct statement (s)

View Solution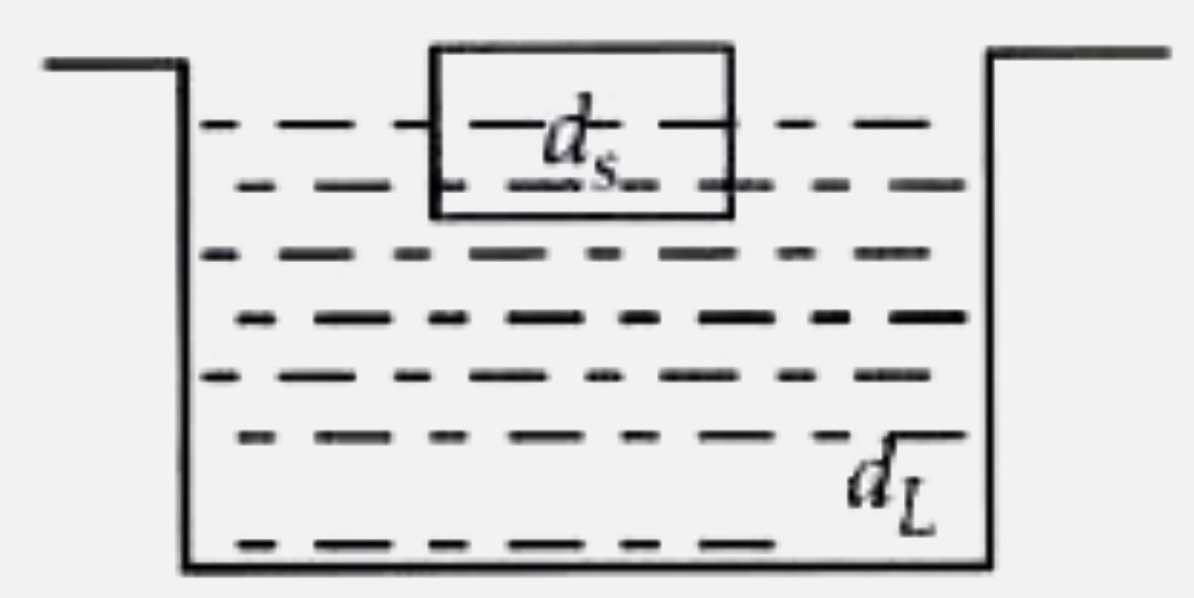
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the apparent weight of the floating body?
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionThe relative density of a material of a body is found by weighing it first in air and then in water. If the weight of he body in air is W1=8.00±N and the weight in water is W2=6.00±0.05N, then the relative density ρr=W1/(W1−W2) with the maximum permissible eror is
View SolutionA solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
View SolutionA body of density ρ is immersed in a liquid of density ρL.State condition when the body will (i) float (ii) sink in liquid.
View SolutionA body of density 2.5g/cm3 is let free in a liquid of density 1.25g/cm3 . The downward acceleration of the of the body while sinking in the liquid is . _______
View SolutionA wooden ball of density D is immersed in water of density d to a depth h//2 below the surface of water and then relased. To what height will the ball jump out of water ?
View Solution
