Two containers of equal volume contain the same gas at pressure and and absolute temperature and , respectively. On joining the vessels, the gas reaches a common pressure and common temperature . The ratio is equal to
The correct Answer is:D
To solve the problem, we will use the ideal gas law and the concept of conservation of moles when two containers are combined. Let's break down the solution step by step.
Step 1: Write the Ideal Gas Law for Each Container
For the first container, we can express the number of moles (μ₁) using the ideal gas law:
μ1=P1VRT1
Where:
- P1 = Pressure in the first container
- V = Volume of the container (equal for both)
- R = Universal gas constant
- T1 = Absolute temperature in the first container
For the second container, the number of moles (μ₂) is given by:
μ2=P2VRT2
Step 2: Total Moles After Joining the Containers
When the two containers are joined, the total number of moles of gas remains the same:
μ=μ1+μ2
Substituting the expressions from Step 1:
μ=P1VRT1+P2VRT2
Step 3: Express the Common Pressure and Temperature
After joining, let the common pressure and temperature be P and T, respectively. The total number of moles can also be expressed as:
μ=P(2V)RT
Since the volume of both containers is equal, the total volume is 2V.
Step 4: Set the Two Expressions for Moles Equal
Equating the two expressions for the number of moles:
P(2V)RT=P1VRT1+P2VRT2
We can cancel V and R from both sides:
2PT=P1T1+P2T2
Step 5: Solve for the Ratio PT
Rearranging the equation gives us:
PT=12(P1T1+P2T2)
Final Result
Thus, the ratio PT is:
PT=P12T1+P22T2
Conclusion
The correct answer is:
PT=P12T1+P22T2
For the first container, we can express the number of moles (μ₁) using the ideal gas law:
μ1=P1VRT1
Where:
- P1 = Pressure in the first container
- V = Volume of the container (equal for both)
- R = Universal gas constant
- T1 = Absolute temperature in the first container
μ2=P2VRT2
When the two containers are joined, the total number of moles of gas remains the same:
μ=μ1+μ2
Substituting the expressions from Step 1:
μ=P1VRT1+P2VRT2
After joining, let the common pressure and temperature be P and T, respectively. The total number of moles can also be expressed as:
μ=P(2V)RT
Since the volume of both containers is equal, the total volume is 2V.
Equating the two expressions for the number of moles:
P(2V)RT=P1VRT1+P2VRT2
We can cancel V and R from both sides:
2PT=P1T1+P2T2
Rearranging the equation gives us:
PT=12(P1T1+P2T2)
Thus, the ratio PT is:
PT=P12T1+P22T2
The correct answer is:
PT=P12T1+P22T2
Similar Questions
Two vessels of volume (V1)and(V2) contain the same ideal gas. The pressures in the vessels are (P1)and(P2) and the temperatures are (T1)and(T2) respectively . The two vessels are now connected to each other through a narrow tube. Assuming that no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection.
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View Solution
Knowledge Check
Two cylinder having m1g and m2g of a gas at pressure P1 and P2 respectively are put in cummunication with each other, temperature remaining constant. The common pressure reached will be
AP1P2(m1+m2)P2m1+P1m2BP1P2m1P2m1+P1m2Cm1m2(P1+P2)P2m1(P1+P2)Dm1m2P2P2m1+P1m2A sample of an ideal gas occupies a volume V at pressure P and absolute temperature T. The masss of each molecule is m, then the density of the gas is
AmKTBPmKTCPkmDPKT
An ideal gas has pressure P, volume V and temperature T. Select the correct option.
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
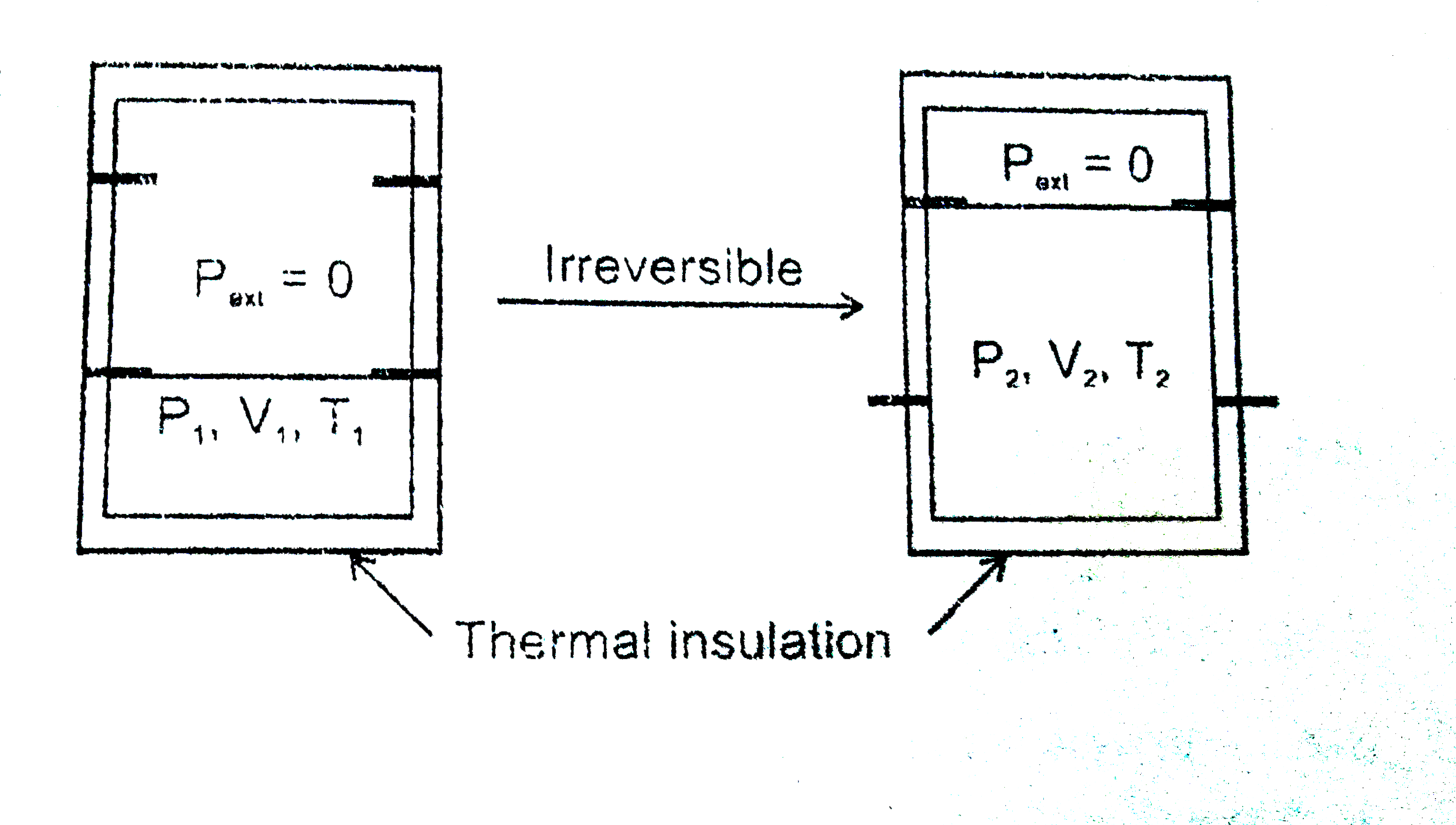
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
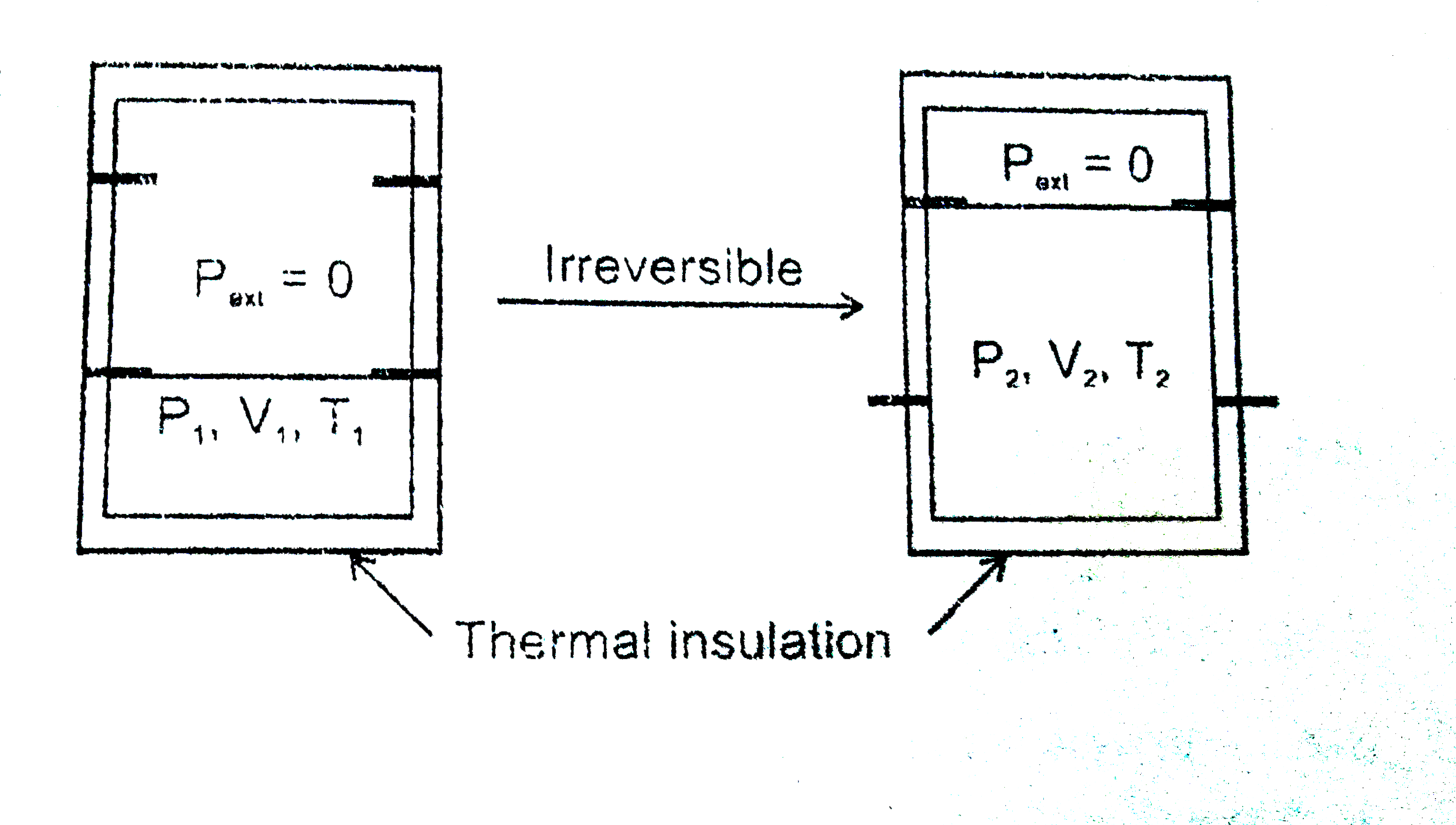
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
View SolutionTwo identical containers joned by a small pipe initially contain the same gas at pressue po and abosolute temperature To. One container is now mantained at the same temperature while the other is heated to 2T0. The commmon pressure of the gases will be
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View Solution