Two billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured?
Inelastic
Elastic
Completely inelastic
Cannot be determined from the information given
The correct Answer is:B
To determine the type of collision that occurred between the two billiard balls, we can analyze the problem step by step using the principles of conservation of momentum and the definition of elastic and inelastic collisions.
1. Identify the Masses and Initial Velocities:
- Let the mass of ball 1 be m1=2m (twice the mass of ball 2).
- Let the mass of ball 2 be m2=m.
- The initial velocity of ball 1 is v and ball 2 is at rest, so its initial velocity u2=0.
2. Final Velocities After Collision:
- After the collision, ball 1 moves with a velocity v′1=v3.
- Let the final velocity of ball 2 be v′2.
3. Apply Conservation of Momentum:
- The total initial momentum before the collision is:
pinitial=m1v+m2u2=(2m)v+(m)(0)=2mv
- The total final momentum after the collision is:
pfinal=m1v′1+m2v′2=(2m)(v3)+mv′2=2mv3+mv′2
- Setting initial momentum equal to final momentum:
2mv=2mv3+mv′2
4. Solve for v′2:
- Rearranging the equation:
2mv−2mv3=mv′2
- Finding a common denominator:
6mv3−2mv3=mv′2
- Simplifying:
4mv3=mv′2
- Dividing by m:
v′2=4v3
5. Determine the Type of Collision:
- The velocities after the collision are v′1=v3 and v′2=4v3.
- Calculate the relative velocity of separation and approach:
- Velocity of separation: v′2−v′1=4v3−v3=3v3=v
- Velocity of approach: v−0=v
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach=vv=1
6. Conclusion:
- Since the coefficient of restitution e=1, this indicates that the collision is perfectly elastic.
Final Answer:
The type of collision that occurred is elastic collision.
- Let the mass of ball 1 be m1=2m (twice the mass of ball 2).
- Let the mass of ball 2 be m2=m.
- The initial velocity of ball 1 is v and ball 2 is at rest, so its initial velocity u2=0.
- After the collision, ball 1 moves with a velocity v′1=v3.
- Let the final velocity of ball 2 be v′2.
- The total initial momentum before the collision is:
pinitial=m1v+m2u2=(2m)v+(m)(0)=2mv
- The total final momentum after the collision is:
pfinal=m1v′1+m2v′2=(2m)(v3)+mv′2=2mv3+mv′2
- Setting initial momentum equal to final momentum:
2mv=2mv3+mv′2
- Rearranging the equation:
2mv−2mv3=mv′2
- Finding a common denominator:
6mv3−2mv3=mv′2
- Simplifying:
4mv3=mv′2
- Dividing by m:
v′2=4v3
- The velocities after the collision are v′1=v3 and v′2=4v3.
- Calculate the relative velocity of separation and approach:
- Velocity of separation: v′2−v′1=4v3−v3=3v3=v
- Velocity of approach: v−0=v
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach=vv=1
- Since the coefficient of restitution e=1, this indicates that the collision is perfectly elastic.
The type of collision that occurred is elastic collision.
Similar Questions
A heavy ball moving with speed v collides with a tiny ball. The collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to
View SolutionVelocity of the ball A after collision with the ball B as shown in the figure is (Assume perfectly inelastic and head - on collision)
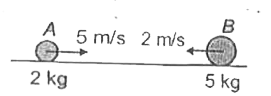
View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
Two identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionConsider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
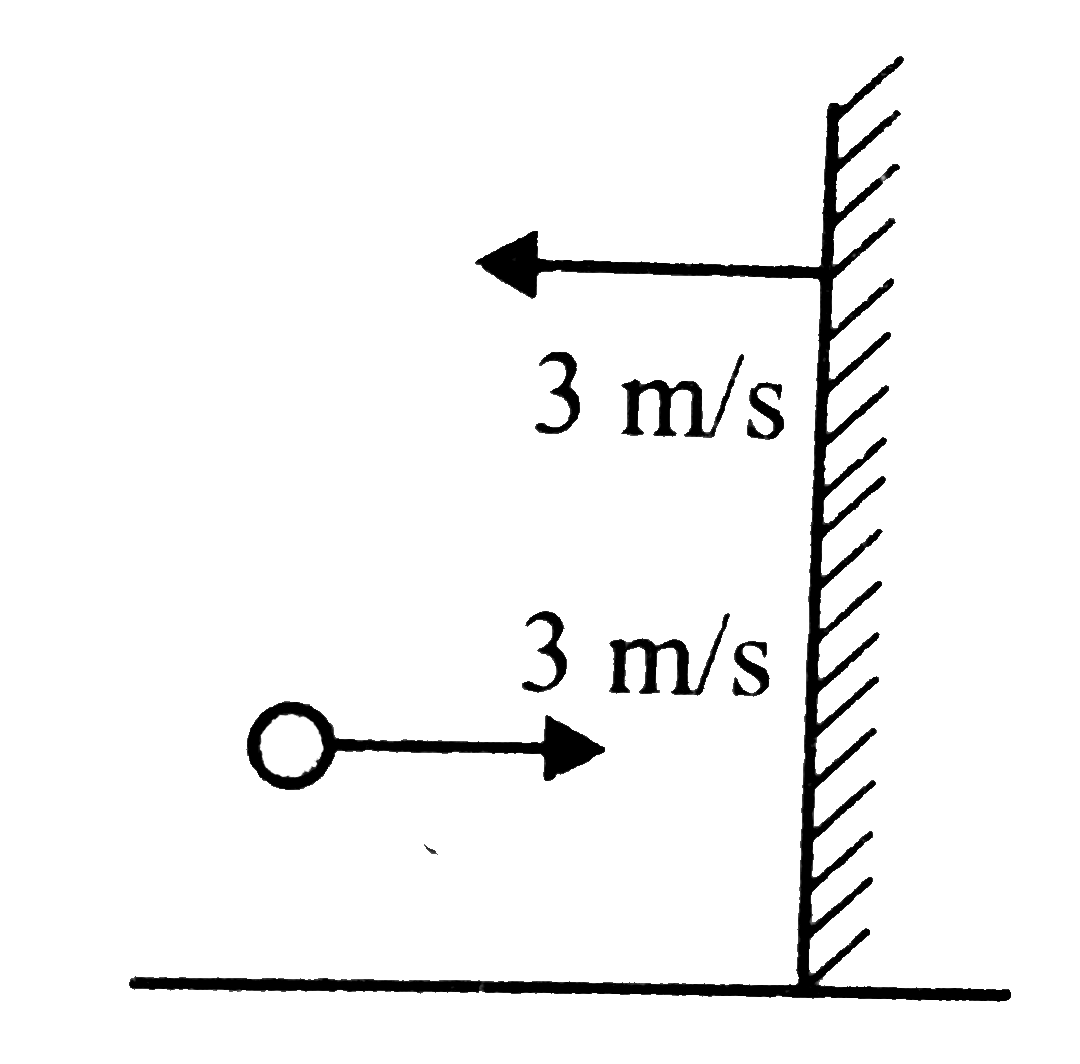
View SolutionA ball of mass 'm' moving with speed 'u' undergoes a head-on elastic collision with a ball of mass 'nm' initially at rest. Find the fraction of the incident energy transferred to the second ball.
View SolutionA ball of mass 4 kg moving on a smooth horizontal surface makes an elastic collision with another ball of mass m at rest in the line of motion of first ball. If after collision first ball moves in the same direction with one fourth of its velocity before collision, then mass of second ball is
View SolutionBall A of mass m strickes a stationary ball B of mass M and undergoes an elastic collision. After collision bill A has a speed one third of its initial speed. The ratio of M/m is
View Solution
