A stone of density 2000 kg m−3 completely immersed in a lake is allowed to sink from rest . If the effect of friction is neglected , than after 4 seconds , the stone will reach a depth of
78.4 m
39.2 m
19.6 m
9.8 m
The correct Answer is:B
To solve the problem step by step, we will analyze the forces acting on the stone and apply the equations of motion.
Step 1: Identify the forces acting on the stone
The stone is subjected to two main forces:
- The weight of the stone (downward): Fg=mg
- The buoyant force (upward): Fb=ρwater⋅V⋅g
Where:
- m is the mass of the stone
- g is the acceleration due to gravity (approximately 9.8m/s2)
- ρwater is the density of water (approximately 1000kg/m3)
- V is the volume of the stone
Step 2: Write the equation of motion
According to Newton's second law, the net force acting on the stone is equal to the mass of the stone times its acceleration:
Fnet=mg−Fb=ma
Substituting the expressions for weight and buoyant force:
mg−ρwater⋅V⋅g=ma
Step 3: Express mass in terms of density and volume
The mass of the stone can be expressed as:
m=ρstone⋅V
Where ρstone=2000kg/m3.
Step 4: Substitute and simplify the equation
Substituting m into the equation gives:
ρstone⋅V⋅g−ρwater⋅V⋅g=ρstone⋅V⋅a
Factoring out V (assuming V≠0):
(ρstone−ρwater)⋅g=ρstone⋅a
Step 5: Solve for acceleration a
Rearranging the equation:
a=(ρstone−ρwater)⋅gρstone
Substituting the known values:
a=(2000−1000)⋅9.82000=1000⋅9.82000=9.82=4.9m/s2
Step 6: Use the equations of motion to find the depth after 4 seconds
Using the equation of motion:
s=ut+12at2
Where:
- u=0 (initial velocity)
- a=4.9m/s2
- t=4s
Substituting the values:
s=0+12⋅4.9⋅(42)=12⋅4.9⋅16=2.45⋅16=39.2m
Final Answer
The stone will reach a depth of 39.2 meters after 4 seconds.
---
The stone is subjected to two main forces:
- The weight of the stone (downward): Fg=mg
- The buoyant force (upward): Fb=ρwater⋅V⋅g
- m is the mass of the stone
- g is the acceleration due to gravity (approximately 9.8m/s2)
- ρwater is the density of water (approximately 1000kg/m3)
- V is the volume of the stone
According to Newton's second law, the net force acting on the stone is equal to the mass of the stone times its acceleration:
Fnet=mg−Fb=ma
Substituting the expressions for weight and buoyant force:
mg−ρwater⋅V⋅g=ma
The mass of the stone can be expressed as:
m=ρstone⋅V
Where ρstone=2000kg/m3.
Substituting m into the equation gives:
ρstone⋅V⋅g−ρwater⋅V⋅g=ρstone⋅V⋅a
Factoring out V (assuming V≠0):
(ρstone−ρwater)⋅g=ρstone⋅a
Rearranging the equation:
a=(ρstone−ρwater)⋅gρstone
Substituting the known values:
a=(2000−1000)⋅9.82000=1000⋅9.82000=9.82=4.9m/s2
Using the equation of motion:
s=ut+12at2
Where:
- u=0 (initial velocity)
- a=4.9m/s2
- t=4s
s=0+12⋅4.9⋅(42)=12⋅4.9⋅16=2.45⋅16=39.2m
The stone will reach a depth of 39.2 meters after 4 seconds.
Similar Questions
A ball falls freely from rest. The ratio of the distance travelled in first, second, third and fourth second is
View SolutionA stone of relative density K is released from rest on the surface of a lake. If viscous effects are lgnored, the stone sinks in water with an acceleration of
View SolutionA stone of 1kg is thrown with a velocity of 20ms−1 across the frozen surface of lake and comes to rest after travelling a distance of 50m. What is the force of friction between the stone and the ice?
View SolutionA stone is dropped from roof of building takes 5 s to reach the ground. The sound of striking is heard after 5.4 second after the stone is dropped. The velocity of sound is
View SolutionA small stone of mass m(=200g) is held under water in a jar and is allowed to fall as shown in fig. the forces acting on stone are also shown.
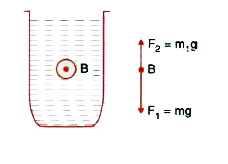
(i) What does F2 represent ?
(ii) What does m1 represent?
(iii) What is the net force acting on stone?
(iv) What is the acceleration of stone as it falls through water? Neglect the force due to viscosity. Assume that the volume of stone
=80cm3, density of water =1.0gcm−3 and acceleration due to gravity g=10ms−2
View SolutionA body of mass 70kg, when completely immersed in water, dispaces 20,00cm3 of water. Find : (i) the weight of body in water and (ii) the relative density of material of body.
View SolutionAn iron block is suspended from a string and is then completely immersed in a container of water. The mass of iron is 1 kg and its density is 7200kg/m3 . What is the tension in the string before and after the iron block is immersed ?
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given θ1=30∘, θ92)=60∘ and h=10m. What are the speeds and time taken by the two stones?
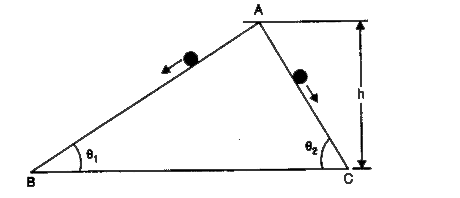
View Solution(b) A stone is thrown from a bridge at an angle of 30∘ down with the horizontal with a velocity of 25 m//s . If the stone strikes the water after 2.5 seconds then calculate the height of the bridge from the water surface (g=9.8m/s2).
View SolutionA ballon starts rising from ground from rest at some constant acceleration. After some time, a storne is dropped from it. If the stone reaches the ground in the same time in which balloon reached the dropping poing from ground, find the acceleration of the balloon.
View Solution
