THE magnitude of maximum accesleration is π times that of maximum velocity of a simble harmonic oscillator The time period of the oscillator. The time period of the oscillator in second is,
4
2
1
0.5
The correct Answer is:B
To solve the problem, we need to find the time period of a simple harmonic oscillator (SHO) given that the magnitude of maximum acceleration is π times that of maximum velocity.
1. Understand Maximum Velocity and Acceleration in SHM:
- The maximum velocity Vmax of a simple harmonic oscillator is given by:
Vmax=Aω
where A is the amplitude and ω is the angular frequency.
- The maximum acceleration amax is given by:
amax=ω2A
2. Set Up the Relationship Given in the Problem:
- According to the problem, the maximum acceleration is π times the maximum velocity:
amax=πVmax
3. Substitute the Expressions for Maximum Velocity and Acceleration:
- Substitute the expressions we have for amax and Vmax:
ω2A=π(Aω)
4. Simplify the Equation:
- We can cancel A from both sides (assuming A≠0):
ω2=πω
5. Rearranging the Equation:
- Rearranging gives:
ω2−πω=0
- Factor out ω:
ω(ω−π)=0
6. Solve for ω:
- This gives us two solutions:
- ω=0 (not physically meaningful for an oscillator)
- ω=π
7. Find the Time Period:
- The time period T of the oscillator is related to the angular frequency ω by:
T=2πω
- Substituting ω=π:
T=2ππ=2 seconds
Conclusion:
The time period of the oscillator is 2 seconds.
- The maximum velocity Vmax of a simple harmonic oscillator is given by:
Vmax=Aω
where A is the amplitude and ω is the angular frequency.
amax=ω2A
- According to the problem, the maximum acceleration is π times the maximum velocity:
amax=πVmax
- Substitute the expressions we have for amax and Vmax:
ω2A=π(Aω)
- We can cancel A from both sides (assuming A≠0):
ω2=πω
- Rearranging gives:
ω2−πω=0
- Factor out ω:
ω(ω−π)=0
- This gives us two solutions:
- ω=0 (not physically meaningful for an oscillator)
- ω=π
- The time period T of the oscillator is related to the angular frequency ω by:
T=2πω
- Substituting ω=π:
T=2ππ=2 seconds
The time period of the oscillator is 2 seconds.
Similar Questions
Knowledge Check
A simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20sA particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A simple harmonic oscillator has a period T and energy E. the amplitude of the oscillator is doubled. Choose the correct answer.
APeriod and energy get doubled.BPeriod gets doubled while energy remains the same.CEnergy gets doubled while period remains the same.Dperiod remains the same and energy becomes four times.
Find the displacement of a simple harmonic oscillator at which its PE is half of the maximum energy of the oscillator.
View SolutionThe maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View SolutionThe velocity-time diagram of a harmonic oscillator is shown in the adjoining figure. The frequency of oscillation is
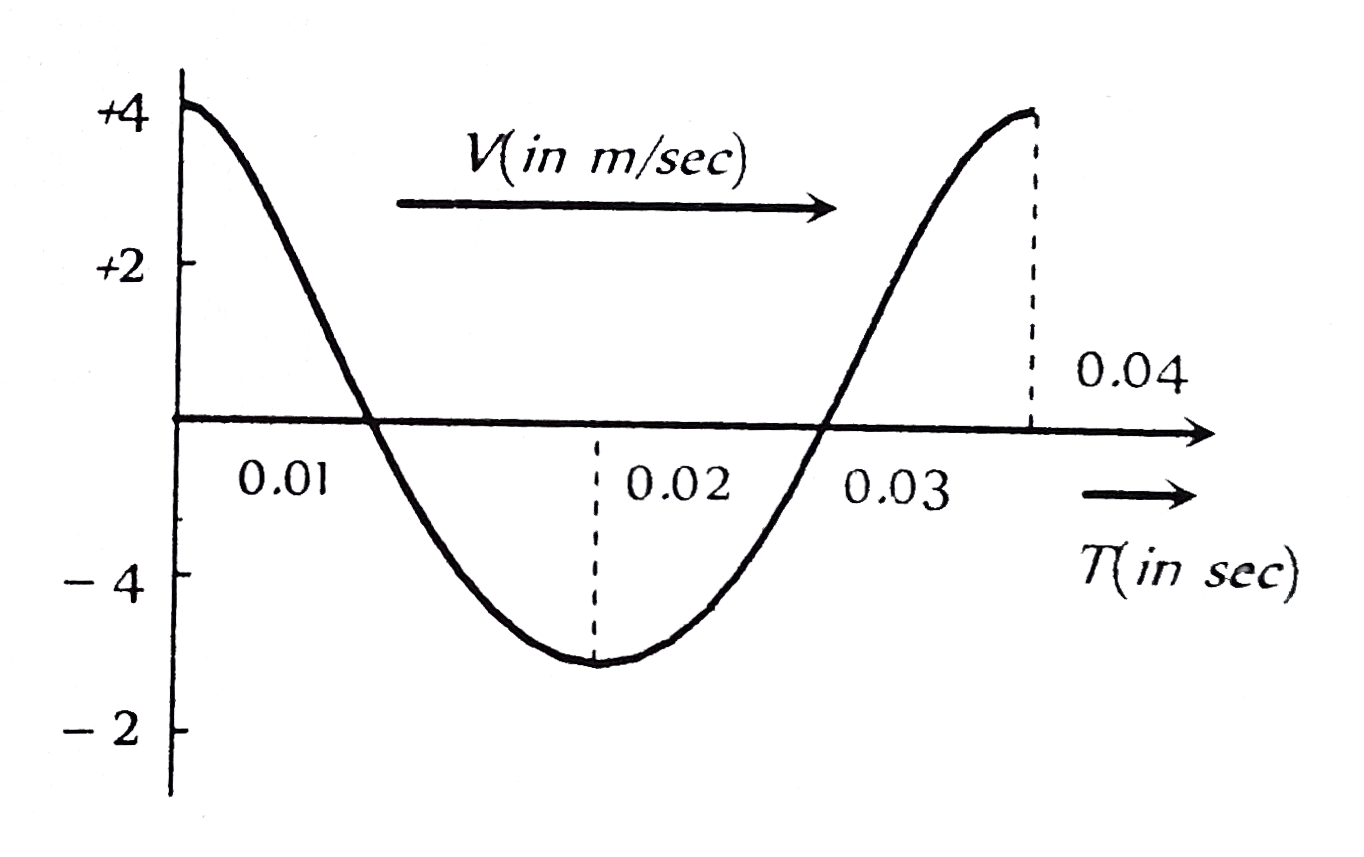
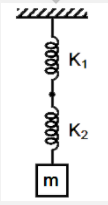
View SolutionTime period of oscillation for given combination will be :
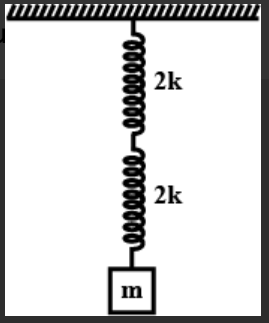
View SolutionThe time period of oscillation of the block as shown in figure is
View Solution
_S01_040_Q01.png)