From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
10√3
20 m
20√3m
40√3
The correct Answer is:C
To find the horizontal range of the projectile, we can use the formula for the range R of a projectile launched at an angle θ with an initial speed u:
R=u2sin(2θ)g
Where:
- u is the initial speed,
- θ is the launch angle,
- g is the acceleration due to gravity (approximately 10m/s2 for this problem).
1. Identify the Given Values:
- Initial speed u=20m/s
- Launch angle θ=60∘
- Acceleration due to gravity g=10m/s2
2. Calculate 2θ:
2θ=2×60∘=120∘
3. Calculate sin(2θ):
- We need to find sin(120∘).
- sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
4. Substitute Values into the Range Formula:
R=(20m/s)2⋅sin(120∘)10m/s2
R=400⋅√3210
5. Simplify the Expression:
R=400⋅√3210=400√320=20√3m
Final Answer:
The horizontal range of the projectile is R=20√3meters.
---
- u is the initial speed,
- θ is the launch angle,
- g is the acceleration due to gravity (approximately 10m/s2 for this problem).
- Initial speed u=20m/s
- Launch angle θ=60∘
- Acceleration due to gravity g=10m/s2
2θ=2×60∘=120∘
- We need to find sin(120∘).
- sin(120∘)=sin(180∘−60∘)=sin(60∘)=√32
R=(20m/s)2⋅sin(120∘)10m/s2
R=400⋅√3210
R=400⋅√3210=400√320=20√3m
The horizontal range of the projectile is R=20√3meters.
Similar Questions
In case of a projectile fired at an angle equally inclined to the horizontal and vertical with velocity (u). The horizontal range is:-
View SolutionThe velocity of projection of oblique projectile is (6ˆi+8ˆj)ms−1 The horizontal range of the projectile is
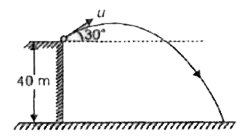
View SolutionFigure shows a projectile thrown with speed u = 20 m/s at an angle 30∘ with horizontal from the top of a building 40 m high. Then the horizontal range of projectile is
View SolutionA projectile is fired from a gun at an angle of 45∘ with the horizontal and with a speed of 20m/s relative to ground. At the highest point in its flight the projectile explodes into two fragments of equal masses. One fragement, whose initial speed is zero falls vertically. How far from the gun does the other fragment land, assuming a level terrain? Take g=10m/s2?
View SolutionA projectile is fired at an angle of 30° to the horizontal with the speed v. If another projectile is projected with the same speed, then at what angle with the horizontal it must be projected so as to have the same range ?
View SolutionA stone projected from ground with certain speed at an angle θ with horizontal attains maximum height h1 when it is projected with same speed at an angle θ with vertical attains height h2. The horizontal range of projectile is
View SolutionA projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
View SolutionThe maximum height attained by a projectile when thrown at an angle θ with the horizontal is found to be half the horizontal range. Then θ is equal to
View SolutionKeeping the velocity of projection constant, the angle of projection is increased from 0° to 90°. Then the horizontal range of the projectile
View SolutionThe range of a projectile, when launched at an angle of 15∘ with the horizontal is 1.5 km. what is the range of the projectile, when launched at an angle of 45∘ to the horizontal with the same speed ?
View Solution
