The correctness of velocity of an electron moving with velocity 50ms−1 is 0.005% . The accuracy with which its position can be measured will be
4634×10−3m
4634×10−5m
4634×10−6m
4634×10−8m
The correct Answer is:B
To solve the problem of determining the accuracy with which the position of an electron can be measured given its velocity and the correctness of that velocity, we can follow these steps:
1. Understand the Given Information:
- Velocity of the electron, V=50ms−1
- Correctness of velocity, ΔV/V×100=0.005%
2. Convert the Correctness Percentage to Decimal:
- Convert 0.005% to decimal form:
0.005%=0.005100=0.00005
3. Calculate the Uncertainty in Velocity (ΔV):
- Use the formula for correctness:
ΔV=V×0.00005
- Substitute the value of V:
ΔV=50×0.00005=0.0025ms−1
4. Use the Heisenberg Uncertainty Principle:
- The uncertainty in position (ΔX) is related to the uncertainty in momentum (ΔP) by the formula:
ΔXΔP≥h4π
- Where ΔP=mΔV and h is Planck's constant (6.63×10−34Js).
- The mass of the electron m is 9.1×10−31kg.
5. Calculate the Uncertainty in Momentum (ΔP):
- Calculate ΔP:
ΔP=mΔV=(9.1×10−31)×(0.0025)=2.275×10−33kg m/s
6. Calculate the Uncertainty in Position (ΔX):
- Rearranging the Heisenberg uncertainty principle gives:
ΔX≥h4πΔP
- Substitute the values:
ΔX≥6.63×10−344π(2.275×10−33)
- Calculate ΔX:
ΔX≥6.63×10−344×3.14×2.275×10−33≈4.63×10−5m
Final Result:
The accuracy with which the position of the electron can be measured is approximately 4.63×10−5m or 4634×10−5m.
- Velocity of the electron, V=50ms−1
- Correctness of velocity, ΔV/V×100=0.005%
- Convert 0.005% to decimal form:
0.005%=0.005100=0.00005
- Use the formula for correctness:
ΔV=V×0.00005
- Substitute the value of V:
ΔV=50×0.00005=0.0025ms−1
- The uncertainty in position (ΔX) is related to the uncertainty in momentum (ΔP) by the formula:
ΔXΔP≥h4π
- Where ΔP=mΔV and h is Planck's constant (6.63×10−34Js).
- The mass of the electron m is 9.1×10−31kg.
- Calculate ΔP:
ΔP=mΔV=(9.1×10−31)×(0.0025)=2.275×10−33kg m/s
- Rearranging the Heisenberg uncertainty principle gives:
ΔX≥h4πΔP
- Substitute the values:
ΔX≥6.63×10−344π(2.275×10−33)
- Calculate ΔX:
ΔX≥6.63×10−344×3.14×2.275×10−33≈4.63×10−5m
The accuracy with which the position of the electron can be measured is approximately 4.63×10−5m or 4634×10−5m.
Similar Questions
Knowledge Check
The wavelength of an electron moving with velocity of 107ms−1 is
A7.27×10−11mB3.55×10−11mC8.25×10−4mD1.05×10−16m
Calculate the wavelength of an electron moving with a velocity of 2.05×107ms−1.
View SolutionThe uncertainty in the position of an electron moving with a velocity of 3×104 cm sec−1 accurate up to 0.011 %
View SolutionIn the figure shown the block B moves with , velocity 10ms−1. The velocity of A in the position shown is
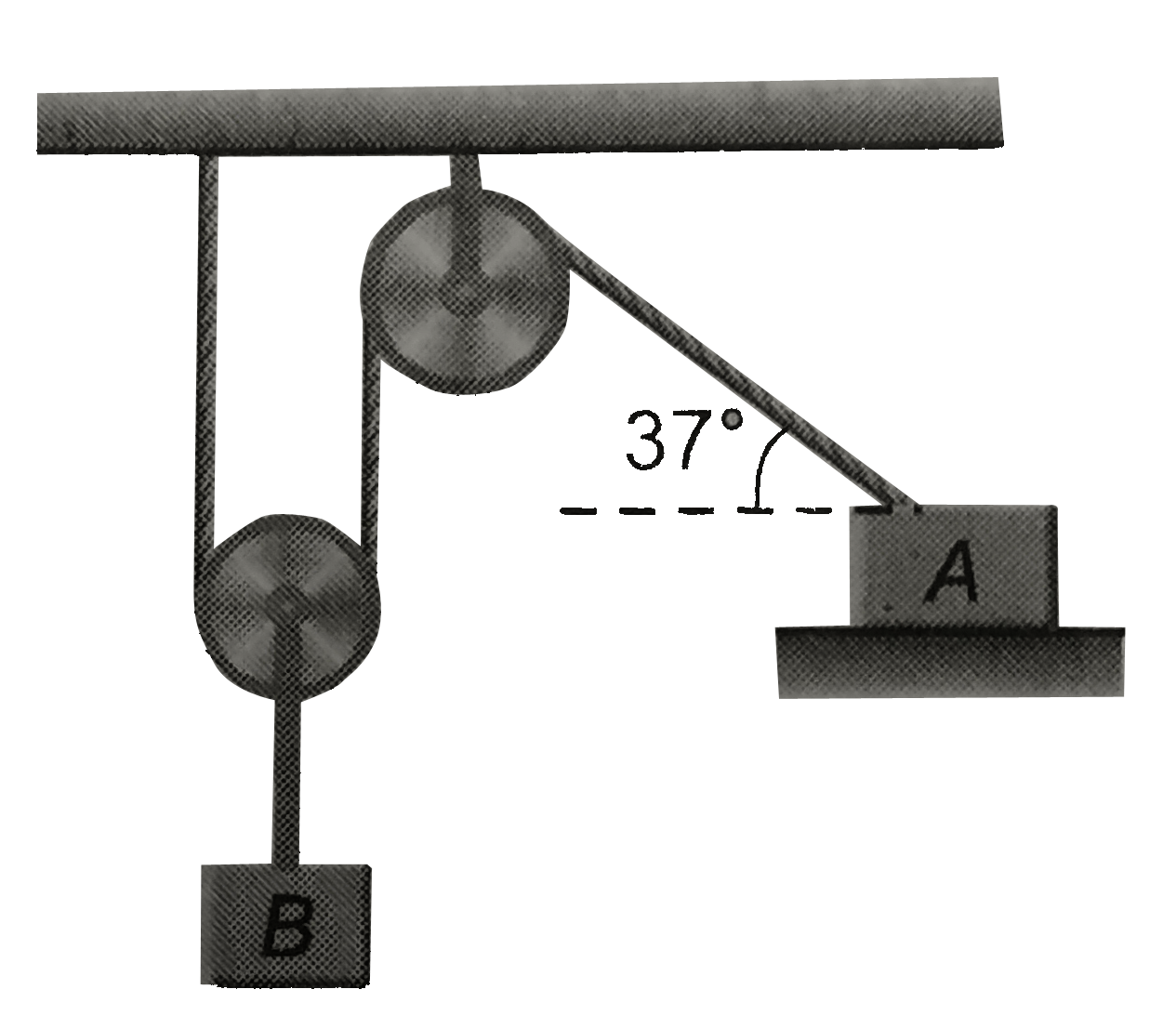
View SolutionA cricket ball of 0.5 kg is moving with a velocity of 100ms−1. The wavelength associated with its motion is :
View SolutionWhat will be de Broglie's wavelength of an electron moving with a velocity of 1.2×105ms−1 ?
View SolutionIn an atom, an electron is moving with a speed of 600m/s with an accuracy of 0.005% . Certainty with which the position of the electron can be localized is :
(h=6.6×10−34kgm2s−1 ,
mass of electron (em)=9.1×10−31kg).
View SolutionA particle of mass 1mg has the same wavelength as an electron moving with a velocity of 3×106ms−1. The velocity of the particle is
View Solution
