A disc of mass M and radius R has a spring of constant k attached to its center , the other end of the spring being fixed to a vertical wall. If the disk rolls without slipping on a level floor, how far to the right does the centre of mass move , if Initially the spring was unstretched and the angular speed of the disc was ω0
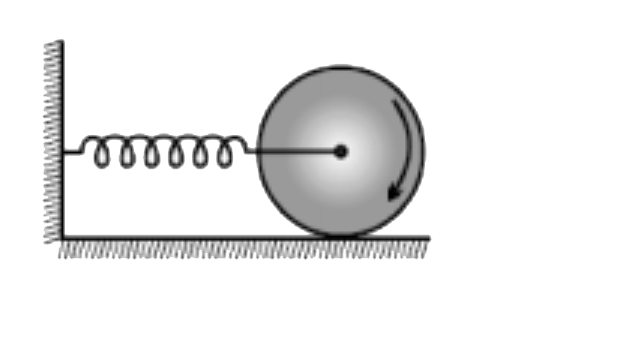
Rω√(2M/3k)
Rω√(3M/2k)
Rω√(M/k)
Rω√(M/2k)
The correct Answer is:B
Step by step video & image solution for A disc of mass M and radius R has a spring of constant k attached to its center , the other end of the spring being fixed to a vertical wall. If the disk rolls without slipping on a level floor, how far to the right does the centre of mass move , if Initially the spring was unstretched and the angular speed of the disc was omega_0 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
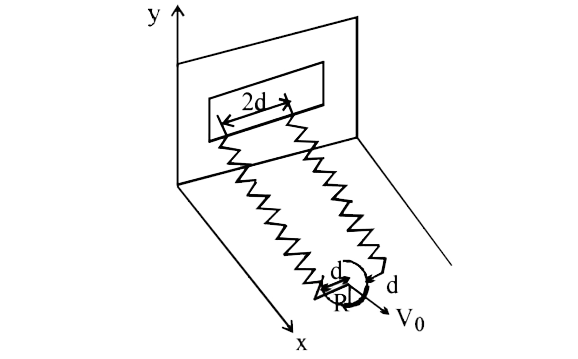
The centre of mass of the disk undergoes simple harmonic motion with angular frequency ω equal to -
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.

The maximum value of V0 for whic the disk will roll without slipping is-
View SolutionOne end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?

View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
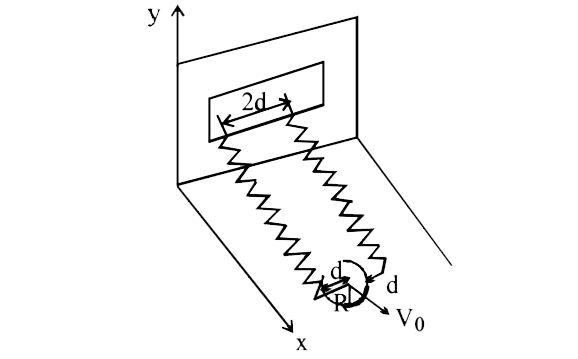
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View SolutionA metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disk of mass 'M' and radius 'R' (< L) is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A) - The disc is not free to rotate about its centre and (case B) - the disc is free to rotate about its centre. The rod-disc system after being released from the same displaced position. Which of the following statement(s) is(are) true?
View Solution
