In Fraunhofer diffraction experiment, L is the distance between screen and the obstacle, b is the size of obstacle and λ is wavelength of incident light. The general condition for the applicability of Fraunhofer diffraction is :
b2Lλ>>1
b2Lλ=1
b2Lλ<<1
b2Lλ≠1
The correct Answer is:C
To determine the general condition for the applicability of Fraunhofer diffraction, we need to analyze the relationship between the size of the obstacle (b), the distance from the obstacle to the screen (L), and the wavelength of the incident light (λ).
1. Understanding Fraunhofer Diffraction:
- Fraunhofer diffraction occurs when both the source of light and the observation screen are at a large distance from the diffracting obstacle. This means that the distances involved (from the source to the obstacle and from the obstacle to the screen) are effectively infinite.
2. Identifying the Parameters:
- Let:
- b = size of the obstacle
- L = distance from the obstacle to the screen
- λ = wavelength of the incident light
3. Condition for Fraunhofer Diffraction:
- The condition for Fraunhofer diffraction can be expressed in terms of the ratio:
b2Lλ
- For Fraunhofer diffraction to be applicable, this ratio must be very small. This is because as L approaches infinity, the term Lλ becomes very large, making the ratio b2Lλ approach zero.
4. Conclusion:
- Therefore, the general condition for the applicability of Fraunhofer diffraction is:
b2Lλ≪1
- This means that b2 must be much less than Lλ.
Final Answer:
The general condition for the applicability of Fraunhofer diffraction is:
b2Lλ≪1
- Fraunhofer diffraction occurs when both the source of light and the observation screen are at a large distance from the diffracting obstacle. This means that the distances involved (from the source to the obstacle and from the obstacle to the screen) are effectively infinite.
- Let:
- b = size of the obstacle
- L = distance from the obstacle to the screen
- λ = wavelength of the incident light
- The condition for Fraunhofer diffraction can be expressed in terms of the ratio:
b2Lλ
- For Fraunhofer diffraction to be applicable, this ratio must be very small. This is because as L approaches infinity, the term Lλ becomes very large, making the ratio b2Lλ approach zero.
- Therefore, the general condition for the applicability of Fraunhofer diffraction is:
b2Lλ≪1
- This means that b2 must be much less than Lλ.
The general condition for the applicability of Fraunhofer diffraction is:
b2Lλ≪1
Similar Questions
In a Young's double slit experiment, the fringe width will remain same, if ( D = distance between screen and plane of slits, d = separation between two slits and λ = wavelength of light used)
View SolutionIn Young's double slit experiment, if the distance between two slits is equal to the wavelength of used light. Then the maximum number of bright firnges obtained on the screen will be
View Solution
Knowledge Check
In Young's double slit experiment, the distance between two sources is 0.1mm. The distance of screen from the sources is 20cm. Wavelength of light used is 5460Å. Then angular position of the first dark fringe is
A0.08∘B0.16∘C0.20∘D0.31∘
The source is at some distance from an obstacle. Distance between obstacle and the point of observation is .b. and wavelength of light is .λ.. Then the distance of nth Fresnel Zone will be at a distance……….from the point of observation.
View SolutionDiffraction of light is observed only, when the obstacle size is-
View SolutionDiffraction of light is observed only, when the obstacle size is-
View SolutionIn a Fraunhofer diffraction experiment at a single slit using a light of wavelength 400 nm, the first minimum is formed at an angle of 30∘. The direction θ of the first secondary maximum is given by :
View SolutionIn a single slit diffraction method, the distance between slit and screen is 1m. The size of the slit is 0.7mm and second maximum is formed at the distance of 2mm from the centre of the screen, then find out the wavelength of light.
View SolutionIf 'b' represents the size of object interacting with light L represents the distance between object and screen X is the wavelength of light then, match the following lists.
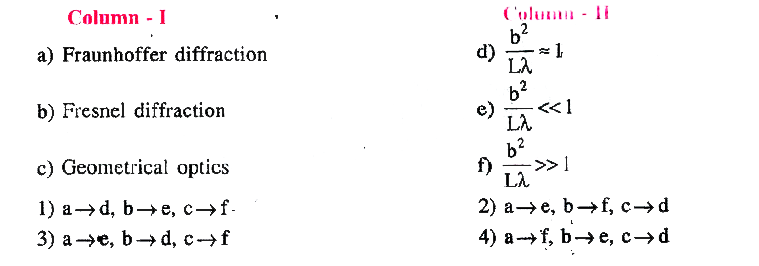
View SolutionIn Young's experiment the distance between two slits is d3 and the distance between the screen and the slits is 3D. The number of fringes in 13 metre on the screen, formed by monochromatic light of wavelength 3λ, will be:
View Solution
