An unbanked circular highway curve on the level ground makes a turn of 90∘. The highway carries traffic at 108 km h−1, and the centripetal force on a vehicle is not to exceed 110 of its weight. What is the approximate minimum length of he curve, in km?
(a)1.41 km
(b)1 km
(c)0.6 km
(d)None of these
The correct Answer is:A
To solve the problem, we need to find the minimum length of a 90-degree unbanked circular highway curve where the centripetal force does not exceed one-tenth of the vehicle's weight.
1. Convert the speed from km/h to m/s:
V=108 km/h=108×1000 m3600 s=30 m/s
2. Set up the centripetal force condition:
The centripetal force Fc required to keep the vehicle moving in a circle is given by:
Fc=mv2r
where m is the mass of the vehicle, v is the velocity, and r is the radius of the curve.
3. Relate the centripetal force to the weight of the vehicle:
The weight W of the vehicle is given by:
W=mg
where g is the acceleration due to gravity (approximately 10 m/s2). According to the problem, the centripetal force should not exceed one-tenth of the weight:
mv2r≤mg10
4. Cancel the mass m from both sides:
v2r≤g10
5. Substitute the values:
Plugging in v=30 m/s and g=10 m/s2:
302r≤1010
900r≤1
6. Solve for the radius r:
Rearranging gives:
r≥900 m
7. Calculate the length of the curve:
The length L of a 90-degree curve (which is one-fourth of a circle) is given by:
L=14×2πr=πr2
Substituting r=900 m:
L=π×9002=450π m
8. Convert the length from meters to kilometers:
L≈450×3.14 m≈1413 m=1.413 km
Final Answer:
The approximate minimum length of the curve is 1.41 km.
---
V=108 km/h=108×1000 m3600 s=30 m/s
The centripetal force Fc required to keep the vehicle moving in a circle is given by:
Fc=mv2r
where m is the mass of the vehicle, v is the velocity, and r is the radius of the curve.
The weight W of the vehicle is given by:
W=mg
where g is the acceleration due to gravity (approximately 10 m/s2). According to the problem, the centripetal force should not exceed one-tenth of the weight:
mv2r≤mg10
v2r≤g10
Plugging in v=30 m/s and g=10 m/s2:
302r≤1010
900r≤1
Rearranging gives:
r≥900 m
The length L of a 90-degree curve (which is one-fourth of a circle) is given by:
L=14×2πr=πr2
Substituting r=900 m:
L=π×9002=450π m
L≈450×3.14 m≈1413 m=1.413 km
The approximate minimum length of the curve is 1.41 km.
Similar Questions
A train rounds an unbanked circular bend of radius 30 m at a speed of 54km/h. The mass of the train is 106 kg. What provides the centripetal force required for this purpose - The engine or the rails ? What is the angle of banking required to prevent wearing out the rails ?
View SolutionFor traffic moving at 60km/h if the radius of the curve is 0.1km what is the correct angle of banking of the road Given g=10m/s2 .
View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
In Q.1, what would be the approximate retardation to be given by jet pack along for safe landing?
View SolutionA circular curve of a highway is designed for traffic moving at 72 km/h. if the radius of the curved path is 100 m, the correct angle of banking of the road should be given by:
View SolutionAn aeroplane is flying at a velocity of 900 km h−1 loops a vertical circular loop. If the maximum force pressing the pilot against the seat is five times his weight, what would be the diameter (in m) of the loop? [g=10ms−2]
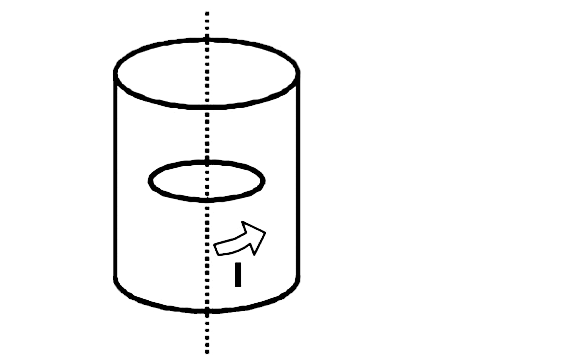
View SolutionA long circular tube of length 10m and radius 0.3m carries a current I along its curved surface as shown . A wire - loop of resistance 0.005ohm and of radius 0.1m is placed inside the tube its axis coinciding with the axis of the tube . The current varies as I=I0cos(300t) where I0 is constant. If the magnetic moment of the loop is Nμ0I0sin(300t), then 'N' is
View SolutionA track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

View SolutionA cyclist speeding at 4.5 km/h on a level road takes a sharp circular turn of radius 3 m without reducing the speed. The coefficient of static friction between the road and the tyres is 0.1.
(i) Will he slip while taking the turn?
(ii) Will he slip if his speed is 9 km/h?
View SolutionA cyclist is riding with a speed of 27kmh−1. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate 0.5ms−1. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View SolutionA cylclist is riding with a speed of 27kmh−1. As he approaches a circular turn on the road of radius 80m, he applies brakes and reduces his speed at the constant rate of 0.5ms−2. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View Solution