In an experiment on photoelectric emission from a metallic surface ,wavelength of incident light m and stopping potential is 2.5V .The threshold frequency of the metal (in Hz) approximately
(Charge of electrons C, Planck's constant ,
The correct Answer is:C
To find the threshold frequency of the metal in the photoelectric emission experiment, we will use the relationship between the stopping potential, the energy of the incident photons, and the threshold frequency.
1. Identify the given values:
- Wavelength of incident light, λ=2×10−7 m
- Stopping potential, V=2.5 V
- Charge of electron, e=1.6×10−19 C
- Planck's constant, h=6.63×10−34 J·s
- Speed of light, c=3×108 m/s
2. Calculate the energy of the incident photons:
The energy of the incident photons can be calculated using the formula:
E=hcλ
Substituting the values:
E=(6.63×10−34J⋅s)×(3×108m/s)2×10−7m
3. Perform the calculation:
E=(6.63×10−34)×(3×108)2×10−7=1.989×10−252×10−7=9.945×10−19J
4. Relate stopping potential to the energy of emitted electrons:
The stopping potential V relates to the kinetic energy of the emitted electrons:
eV=E−E0
where E0 is the work function of the metal. Rearranging gives:
E0=E−eV
5. Calculate the work function E0:
Substituting the values:
E0=9.945×10−19−(1.6×10−19×2.5)
E0=9.945×10−19−4.0×10−19=5.945×10−19J
6. Find the threshold frequency f0:
The threshold frequency f0 can be calculated using the work function:
E0=hf0⟹f0=E0h
Substituting the values:
f0=5.945×10−196.63×10−34≈8.96×1014Hz
7. Round to the nearest significant figure:
The approximate threshold frequency is:
f0≈9×1014Hz
Final Answer:
The threshold frequency of the metal is approximately 9×1014Hz.
---
- Wavelength of incident light, λ=2×10−7 m
- Stopping potential, V=2.5 V
- Charge of electron, e=1.6×10−19 C
- Planck's constant, h=6.63×10−34 J·s
- Speed of light, c=3×108 m/s
The energy of the incident photons can be calculated using the formula:
E=hcλ
Substituting the values:
E=(6.63×10−34J⋅s)×(3×108m/s)2×10−7m
E=(6.63×10−34)×(3×108)2×10−7=1.989×10−252×10−7=9.945×10−19J
The stopping potential V relates to the kinetic energy of the emitted electrons:
eV=E−E0
where E0 is the work function of the metal. Rearranging gives:
E0=E−eV
Substituting the values:
E0=9.945×10−19−(1.6×10−19×2.5)
E0=9.945×10−19−4.0×10−19=5.945×10−19J
The threshold frequency f0 can be calculated using the work function:
E0=hf0⟹f0=E0h
Substituting the values:
f0=5.945×10−196.63×10−34≈8.96×1014Hz
The approximate threshold frequency is:
f0≈9×1014Hz
The threshold frequency of the metal is approximately 9×1014Hz.
Similar Questions
Knowledge Check
In a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
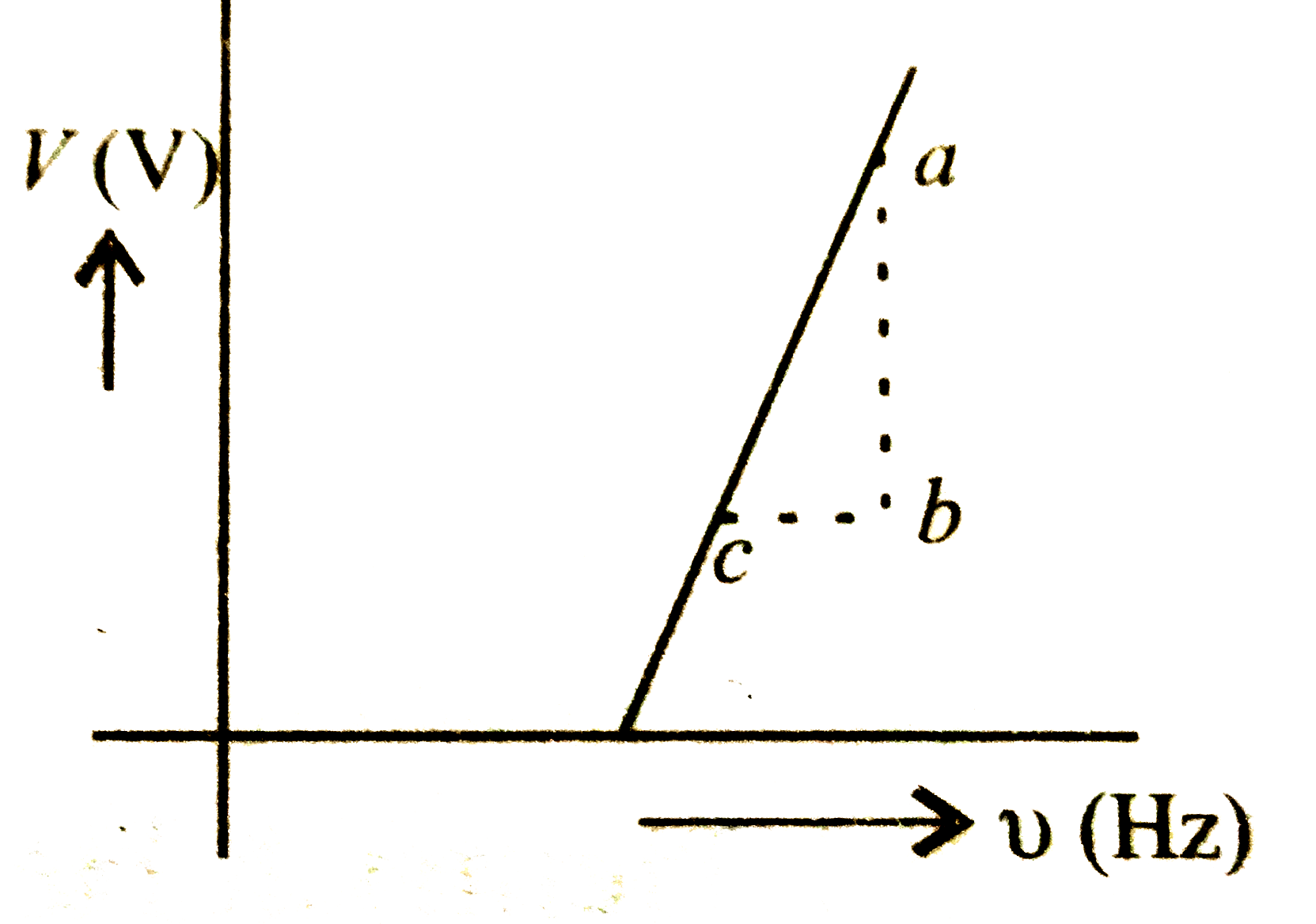AeabbcBecbacCeacbcDeacab
The de - Broglie wavelength of a ball of mass 120 g moving at a speed of 20 m s−1 is (Planck's constant h=6.6×10−34Js)
View SolutionThe threshold frequency for photo electric effect for a metal surface is found to be 4.8×1016 Hz. The stopping potential required when the metal is irradiated by radiation of frequency 5.6×1016 Hz is (taking h=6.6×10−34Js and c=1.6×10−19C )
View SolutionWhat is the number of significant figures in Avogadro's number (6.0×1023) and Planck's constant (6.62×10−34Js).
View SolutionThe threshold wavelength for emission of photoelectrons from a metal surface is 6×10−7 m. What is the work function of the material of the metal surface ?
View SolutionIn a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
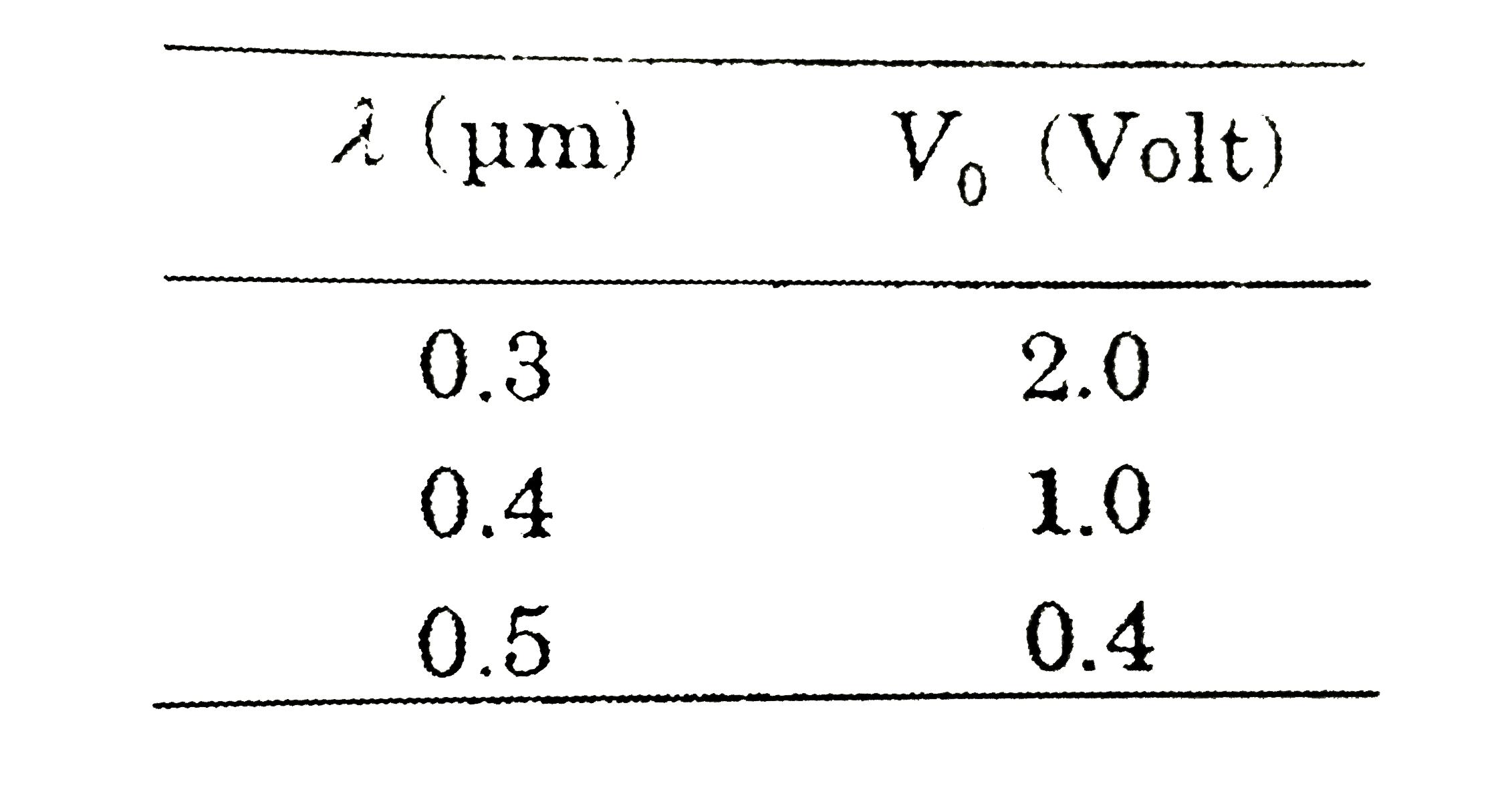
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment is
View SolutionThe maximum kinetic energy of the photoelectrons is found to be 6.63×10−19J, when the metal is irradiated with a radiation of frequency 2×1015Hz. The threshold frequency of the metal is about:
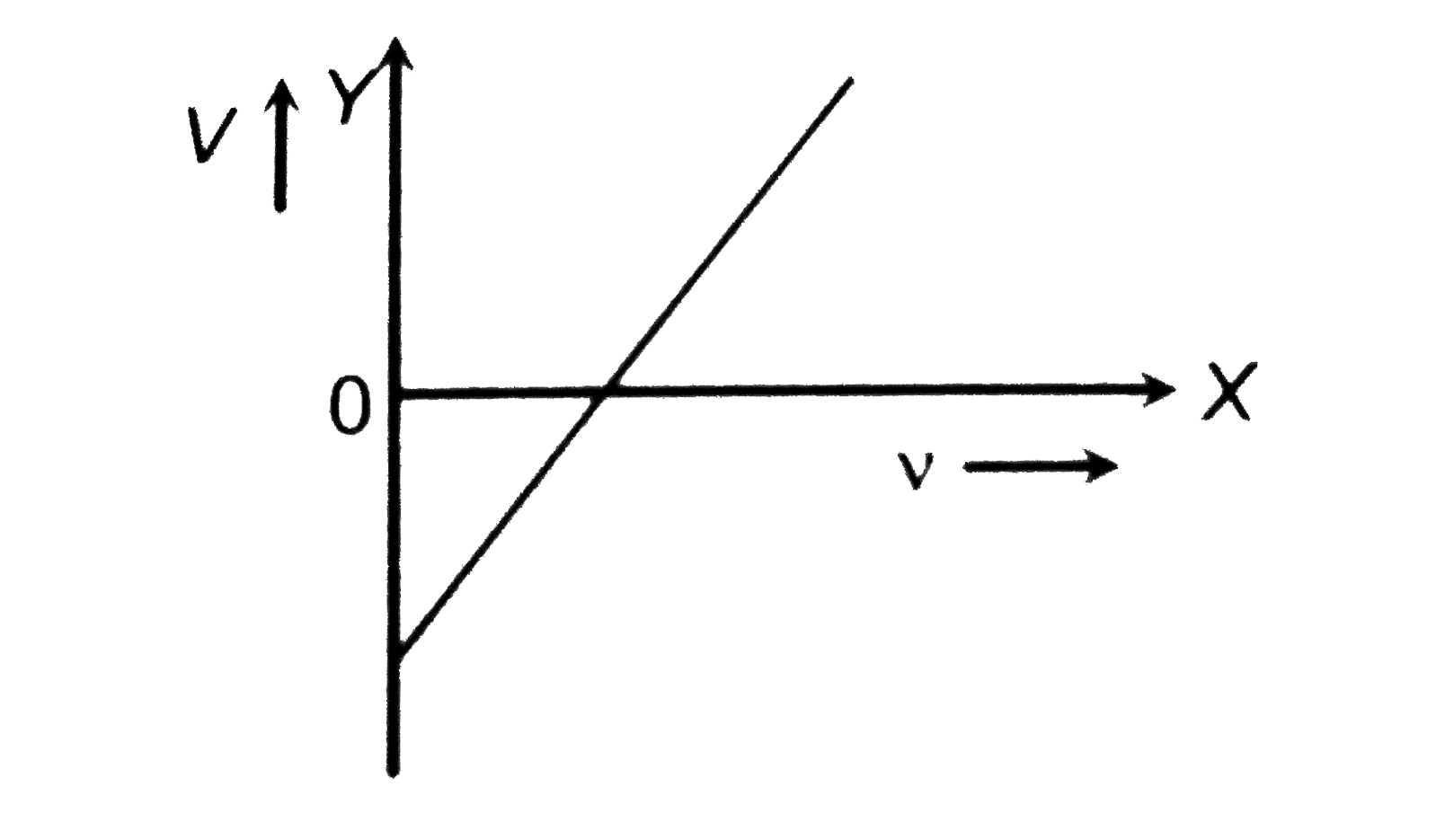
View SolutionThe stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
View Solution