Two bulbs consume the same power when operated at 200 V and 300 V respectively. When these bulbs are connected in series across a DC source of 400 V, then the ratio of power consumed across them is
23
32
49
94
The correct Answer is:C
To solve the problem, we need to find the ratio of power consumed by two bulbs when connected in series across a DC source of 400 V. The bulbs consume the same power when operated at 200 V and 300 V respectively.
1. Understanding Power Consumption:
The power consumed by an electrical device can be expressed using the formula:
P=V2R
where P is the power, V is the voltage, and R is the resistance.
2. Setting Up the Equations:
For the first bulb (operating at 200 V):
P1=2002R1
For the second bulb (operating at 300 V):
P2=3002R2
Since both bulbs consume the same power:
2002R1=3002R2
3. Finding the Resistance Ratio:
Rearranging the equation gives:
R1R2=20023002=(200300)2=(23)2=49
Thus, we have:
R1:R2=4:9
4. Connecting Bulbs in Series:
When the bulbs are connected in series, the same current I flows through both. The total voltage across the series connection is 400 V, and the voltage across each bulb can be expressed as:
V1=IR1andV2=IR2
The total voltage is:
V1+V2=400⇒IR1+IR2=400⇒I(R1+R2)=400
5. Calculating Power in Series:
The power consumed by each bulb can be expressed as:
P1=I2R1andP2=I2R2
The ratio of the power consumed by the two bulbs is:
P1P2=I2R1I2R2=R1R2
Since we found R1:R2=4:9, we have:
P1P2=49
Final Answer:
The ratio of power consumed across the two bulbs when connected in series across a 400 V source is:
P1P2=49
The power consumed by an electrical device can be expressed using the formula:
P=V2R
where P is the power, V is the voltage, and R is the resistance.
For the first bulb (operating at 200 V):
P1=2002R1
For the second bulb (operating at 300 V):
P2=3002R2
Since both bulbs consume the same power:
2002R1=3002R2
Rearranging the equation gives:
R1R2=20023002=(200300)2=(23)2=49
Thus, we have:
R1:R2=4:9
When the bulbs are connected in series, the same current I flows through both. The total voltage across the series connection is 400 V, and the voltage across each bulb can be expressed as:
V1=IR1andV2=IR2
The total voltage is:
V1+V2=400⇒IR1+IR2=400⇒I(R1+R2)=400
The power consumed by each bulb can be expressed as:
P1=I2R1andP2=I2R2
The ratio of the power consumed by the two bulbs is:
P1P2=I2R1I2R2=R1R2
Since we found R1:R2=4:9, we have:
P1P2=49
The ratio of power consumed across the two bulbs when connected in series across a 400 V source is:
P1P2=49
Similar Questions
Two bulbs consume same energy when operated at 200Vand300V , respectively . When these bulbs are connected in series across a dc source of 500V, then
View SolutionIf two bulbs of power 60 W and 100 W respectively each rated 110 V are connected in series with the supply of 220 V, then
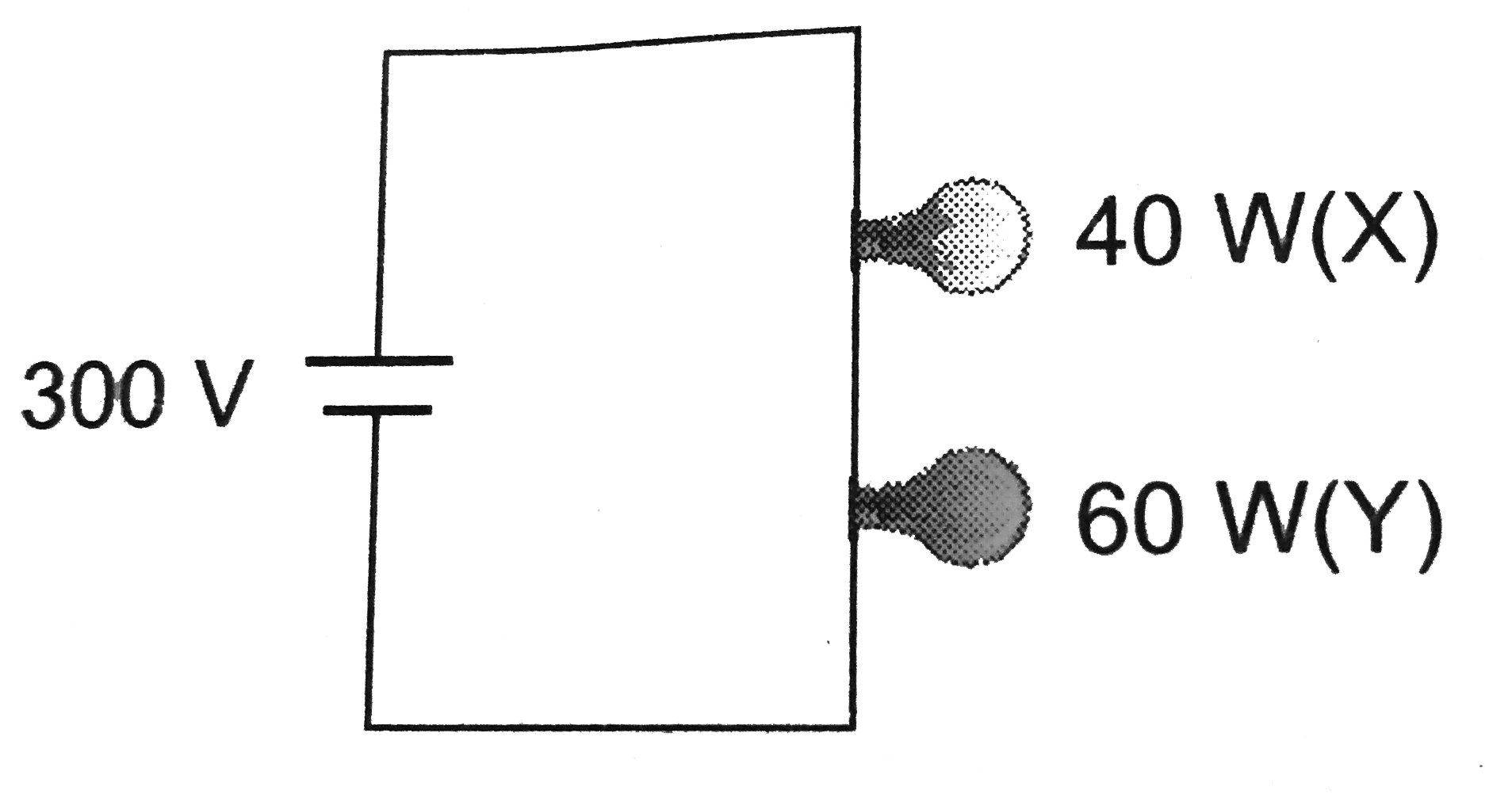
View SolutionTwo bulbs X and Y having same voltage rating and of power 40 watt and 60 watt respectively are connected in series across a potential difference of 300 volt, then
View SolutionTwo bulbs A and B are rated 100 W, 120 V and 10 W, 120 V respectively. They are connected in parallel across a 120 V source.
Find the current in each bulb.
View SolutionTwo bulbs of rated power 60W and 100W same specified voltage 220 V are connected in series to a 440 V DC source
View SolutionTwo bulbs A and B are rated 100 W, 120 V and 10 W, 120 V respectively. They are connected across a 120 V source in series.
Calculate the current through each bulb.
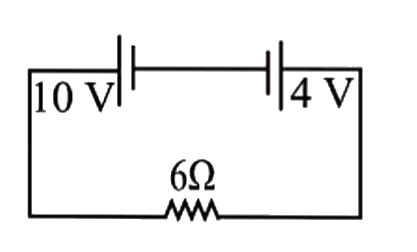
View SolutionThe power consumed by the 4 V battery is
View SolutionTwo bulbs are marked 220 V, 100 W and 220 V, 50W respectively. They are connected in series to 220 V mains. Find the ratio of heats generated in them.
View SolutionTwo bulbs A and B are rated 100 W, 120 V and 10 W, 120 V respectively. They are connected across a 120 V source in series.
Which bulb will consume more power ?
View SolutionTwo bulbs when connected in parallel to a source take 60 W each, the power consumed, when they are connected in series with the same source is
View Solution
