A book of weight is pressed between two hands and each hand exerts a force of . If the block just starts to slide down Coefficient of friction is .
The correct Answer is:0.25
To find the coefficient of friction when a book of weight 20 N is pressed between two hands, each exerting a force of 40 N, we can follow these steps:
1. Identify the Forces Acting on the Book:
- The weight of the book (W) is acting downwards, which is given as 20 N.
- Each hand exerts a force of 40 N, which creates a normal force (N) on the book.
2. Calculate the Total Normal Force:
- Since the book is pressed from both sides, the total normal force (N) acting on the book is the sum of the forces exerted by both hands:
N=40N+40N=80N
3. Understand the Condition for Sliding:
- The book will start to slide when the frictional force (F_f) is equal to the weight of the book (W). The frictional force can be expressed in terms of the coefficient of friction (μ) and the normal force (N):
Ff=μ⋅N
4. Set Up the Equation:
- At the point of sliding, the weight of the book is equal to the frictional force:
W=Ff
- Substituting the expressions, we get:
20N=μ⋅80N
5. Solve for the Coefficient of Friction (μ):
- Rearranging the equation to solve for μ gives:
μ=20N80N=14=0.25
Final Answer:
The coefficient of friction (μ) is 0.25.
- The weight of the book (W) is acting downwards, which is given as 20 N.
- Each hand exerts a force of 40 N, which creates a normal force (N) on the book.
- Since the book is pressed from both sides, the total normal force (N) acting on the book is the sum of the forces exerted by both hands:
N=40N+40N=80N
- The book will start to slide when the frictional force (F_f) is equal to the weight of the book (W). The frictional force can be expressed in terms of the coefficient of friction (μ) and the normal force (N):
Ff=μ⋅N
- At the point of sliding, the weight of the book is equal to the frictional force:
W=Ff
- Substituting the expressions, we get:
20N=μ⋅80N
- Rearranging the equation to solve for μ gives:
μ=20N80N=14=0.25
The coefficient of friction (μ) is 0.25.
Similar Questions
A body of mass M is pressed between two hands. Each hand exerts a horizontal force F. The net horizontal force acting on the body is
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of 50 N is pressed normally against a wall as shown. The frictional force acting on the block is :
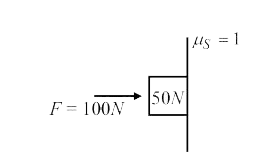 ]
]
View SolutionA man holds a 2 kg book between his palms. so that each hand exerts the same horizontal force on the book. The coefficient of static friction between the palms and the book is 0.4 and g = 10ms−2. If the book is prevented from falling, the least force exerted by each hand on the book is
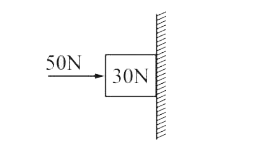
View SolutionA block of weight 30 N is in contact with a rough wall. A force of 50 N is applied as shown in the figure. Find the coefficient of static friction between the wall and the block assuming the block is just about to slip.
View SolutionA20 kg block is initally at rest. A 75 N force is required to set the block in motion. After the motion starts, a force of 60 N is required to keep the block moving with constant speed. The coefficient of static friction is
View SolutionA block of 10kg is pulled at a constant speed on a rough horizontal plane by a force of 20N. Calculate the coefficient of friction ?
View SolutionAn eraser weighing 2N is pressed against the black board with a force of 5N. If the coefficient of friction is 0.4. How much force parallel to the black board is required to slide the eraser upwards
View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View Solution
