Two identical systems, with heat capacity at a constant volume that varies as Cv=bT3 (where b is a constant) are thermally isolated. Initially, one system is at a temperature 100 K and the other is at 200K. The systems are then brought to thermal contact and the combined system is allowed reach thermal equilibrium. If T40=n×108 then what will be the value of n, where T0 is the final temperature in kelvin?
The correct Answer is:8.5
To solve the problem, we need to find the final equilibrium temperature T0 when two identical systems with heat capacities that vary as Cv=bT3 are brought into thermal contact. One system starts at 100 K and the other at 200 K.
1. Understanding the Internal Energy Change:
The change in internal energy dU for a system at constant volume is given by:
dU=CvdT
For our systems, we can express this as:
dU=bT3dT
2. Calculating Internal Energy for System 1:
For the first system (initially at 100 K), the internal energy change from 100 K to T0 is:
U1=∫T0100bT3dT
Evaluating this integral:
U1=b(T44)T0100=b(T404−10044)
Simplifying gives:
U1=b4(T40−1004)
3. Calculating Internal Energy for System 2:
For the second system (initially at 200 K), the internal energy change from T0 to 200 K is:
U2=∫200T0bT3dT
Evaluating this integral:
U2=b(T44)200T0=b(20044−T404)
Simplifying gives:
U2=b4(2004−T40)
4. Setting Internal Energies Equal:
At thermal equilibrium, the total internal energy before contact equals the total internal energy after contact:
U1+U2=0
Therefore, we can set:
b4(T40−1004)=b4(2004−T40)
Canceling b4 from both sides gives:
T40−1004=2004−T40
5. Rearranging the Equation:
Rearranging the equation gives:
2T40=2004+1004
Now, we calculate 2004 and 1004:
2004=(2×102)4=16×108
1004=(102)4=108
Therefore:
2T40=16×108+1×108=17×108
6. Finding T40:
Dividing both sides by 2 gives:
T40=172×108
7. Identifying n:
From the problem, we have T40=n×108. Thus:
n=172=8.5
Final Answer:
The value of n is 8.5.
The change in internal energy dU for a system at constant volume is given by:
dU=CvdT
For our systems, we can express this as:
dU=bT3dT
For the first system (initially at 100 K), the internal energy change from 100 K to T0 is:
U1=∫T0100bT3dT
Evaluating this integral:
U1=b(T44)T0100=b(T404−10044)
Simplifying gives:
U1=b4(T40−1004)
For the second system (initially at 200 K), the internal energy change from T0 to 200 K is:
U2=∫200T0bT3dT
Evaluating this integral:
U2=b(T44)200T0=b(20044−T404)
Simplifying gives:
U2=b4(2004−T40)
At thermal equilibrium, the total internal energy before contact equals the total internal energy after contact:
U1+U2=0
Therefore, we can set:
b4(T40−1004)=b4(2004−T40)
Canceling b4 from both sides gives:
T40−1004=2004−T40
Rearranging the equation gives:
2T40=2004+1004
Now, we calculate 2004 and 1004:
2004=(2×102)4=16×108
1004=(102)4=108
Therefore:
2T40=16×108+1×108=17×108
Dividing both sides by 2 gives:
T40=172×108
From the problem, we have T40=n×108. Thus:
n=172=8.5
The value of n is 8.5.
Similar Questions
V=k(PT)0.33 where k is constant. It is an,
View SolutionCan a system be heated and its temperature ramains constant ?
View SolutionA system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
View SolutionA thermally isolated gaseous system can exchange energy with the surroundings. The mode of energy may be
View SolutionFor an ideal gas the molar heat capacity varies as C=CV+3aT2. Find the equation of the process in the variables (T,V) where a is a constant.
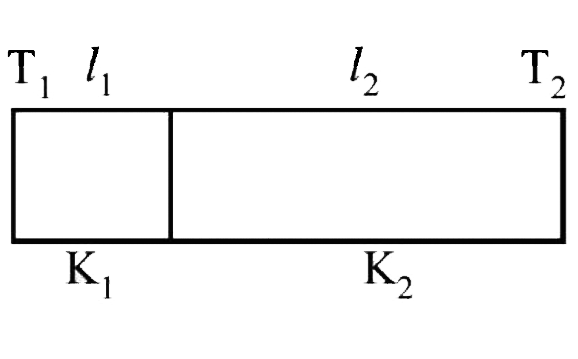
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionThe molar heat capacity of an ideal gas in a process varies as C=CV+αT2 (where CV is mola heat capacity at constant volume and α is a constant). Then the equation of the process is
View SolutionIncrease in enthalpy of the surroundings is equal to decrease in enthalpy of the system. Will the temperature of system and surroundings be the same when they are in thermal equilibrium ?
View SolutionA system absorbs 10kJ of heat at constant volume and its temperature rises from 270C to 370C. The ΔE of reaction is
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View Solution
